[NeRF][이론] Neural Radiance Fields for View Synthesis 개념 설명과 논문 리뷰
들어가기에 앞서..
- 이 글은 EVCC 2020의 “NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis” 논문을 바탕으로 작성되었습니다.
- 논문 링크: https://arxiv.org/abs/2003.08934
- 이 글은 단순히 논문을 순서대로 해석한 글이 아니라, NeRF를 하나부터 열까지 이해하실 수 있도록 기초 개념부터 시작해서 점점 자세한 내용을 설명하는 식으로 재구성하여 작성되었습니다.
목차
순서대로 읽으시는 것을 권장드립니다!
| 서론 | |
| 1. Implicit Neural Representation | 👉바로가기 |
| 2. NeRF 개요 | 👉바로가기 |
| 본론1 (큰 그림 이해하기) | |
| 3. Ray와 Volume Rendering 개요 | 👉바로가기 |
| 4. NeRF의 Training및 Infering 과정 요약 | 👉바로가기 |
| 본론2 (자세히 이해하기) | |
| 5. Hierarchical Volume Sampling | 👉바로가기 |
| 6. Positional Encoding | 👉바로가기 |
| 7. MLP Structure | 👉바로가기 |
| 8. NeRF Volume Rendering | 👉바로가기 |
| 9. Loss Computation | 👉바로가기 |
| 마무리 | |
| 10. 기존 모델과 비교 | 👉바로가기 |
| 11. 결론 및 개선점 | 👉바로가기 |
I. 서론
1. Implicit Neural Representation

레오나르도 다 빈치의 대표작 ‘모나리자’입니다. 1503년도에 레오나르도 다 빈치는 이 그림을 목제 패널에 물감으로 그렸습니다. 이 그림 원본은 목제 패널 위에 유채(油彩)로 ‘표현(represent)’ 되었다고 볼 수 있죠.
하지만 우리는 지금 이 그림을 루브르 박물관에서 보고 있는 것이 아니라 컴퓨터 화면 속에서 보고 있습니다. 디지털 상에서 ‘그림’이라는 정보는 어떻게 표현되었다고 볼 수 있을까요? ‘픽셀(pixel)’로써 표현되었습니다. 이 웹 페이지에 업로드 된 모나리자 그림은 300x447개의 픽셀로 표현된 상태입니다. 각 픽셀은 R,G,B정보를 갖고 있죠.

디지털 상에서 물체는 pixel, vector, voxel, point cloud, mesh 등 다양한 방식으로 표현될 수 있습니다. 이러한 표현 방식은 ‘Explicit(분명한)’ 하다고 할 수 있습니다. 왜냐하면 특정 위치의 색상 정보를 어떤 픽셀이, 또는 어떤 voxel이 가지고 있는지 분명하게 알 수 있기 때문이죠.
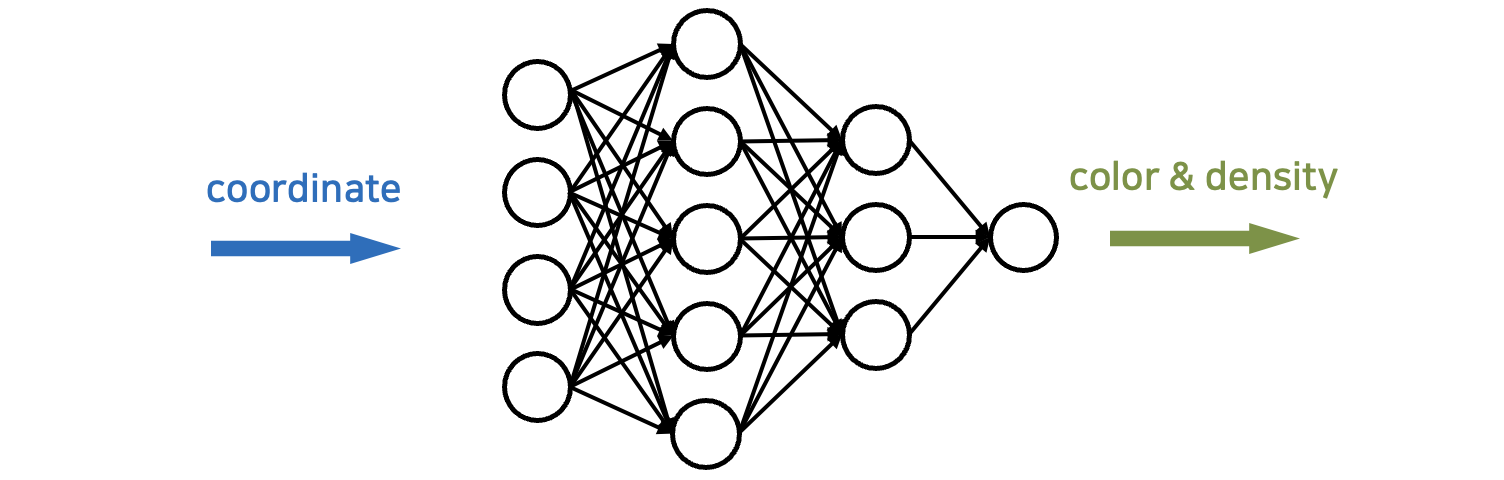
이러한 전통적인 representation 방식을 뛰어넘어 neural network를 통해서도 정보를 저장할 수 있습니다. 이 neural network는 특정 좌표를 input으로 넣으면 해당 좌표에 대한 RGB컬러 등의 정보를 output으로 출력해 주는 neural network입니다. 이 경우 Neural network의 파라미터들이 특정 이미지나 물체나 동영상 등의 정보를 담고 있으며, 정보가 neural network의 파라미터들로써 ‘표현(represent)’된다고 볼 수 있습니다.
이렇게 neural network를 통해 정보를 표현하는 것을 ‘implicit(암시된) representation’이라고 합니다. Implicit representation은 각 neuron의 파라미터(weight, bias)들로써 데이터를 저장하기 때문에, 특정 부분의 rgb값이 어디에 담겼는지 그리고 각각의 파라미터가 어떤 의미를 갖고 있는지 인간이 해석할 수 없기 때문에 implicit(암시된)이라는 용어가 붙었다고 보시면 됩니다.
그렇다면 implicit neural representation이 기존 방식에 비해 갖는 장점이 무엇일까요? 첫 번째로 저장 공간상의 이점이 있습니다. 3차원 데이터의 경우 voxel 이나 point cloud로써 저장하려면, 3차원상의 모든 점마다 색상값 또는 투명도값을 담아야 하기 때문에 무척 많은 저장 공간을 요구합니다. 하지만 neural network를 통해 저장하면, neural network의 각 unit에 존재하는 파라미터값이 모든 데이터를 함축적으로 담고 있기 때문에 상대적으로 저장 공간을 줄일 수 있습니다.
두 번째로, 저장 공간이 컨텐츠와 상관없이 일관적이며, 예측 가능합니다. Neural network를 training하기 전 사전에 몇 개의 layer를 사용하고 layer당 몇 개의 unit을 사용할 지 정하면, 메모리를 딱 그만큼만 사용하게 됩니다. 3D 모델을 저장하던, 2D 이미지를 저장하던 상관없이 말이죠.
하지만, 기존 방식에 비해 데이터를 읽어오는 속도가 느리다는 단점이 있습니다. 매 좌표마다 neural network의 forward연산을 수행하여야만 output값(color등)을 얻을 수 있기 때문이죠.
NeRF(Neural Radiance Field)는 하나의 정적인 3D 데이터에 대해 implicit neural representation을 적용한 것입니다. NeRF가 무엇이고 어떤 원리가 숨어 있는지 지금부터 같이 알아보도록 해요.
2. NeRF 개요
NeRF란 무엇일까요?
NeRF는 3D 공간 내 입자들의 color값과 density값을 neural network의 파라미터로 표현하는 것 + 해당 정보를 원하는 view에 맞추어 렌더링 하는 것 입니다. 1단원에서 언급한 용어를 빌리자면, 3D 데이터를 explicit하게 voxel 또는 point cloud으로 나타내는 것이 아니라, 딥러닝을 통해 학습된 MLP (multi-layer perceptron) 상에서 (implicit하게) 3D 데이터를 reconstruct하는 것이라고 볼 수 있죠.
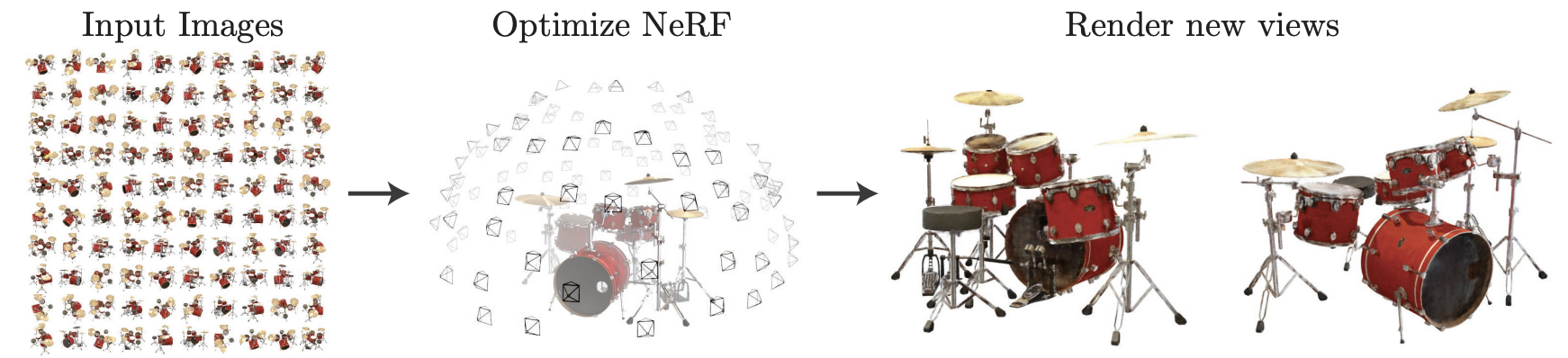
NeRF모델의 학습은 물체에 대해 다양한 각도에서 촬영된 사진을 가지고 일어납니다. 학습된 NeRF모델이 있다면 우리가 물체를 특정 시점에서 바라봤을 때 어떤 색상값이 보이는지 query할 수 있습니다. 쉽게 말해, 원하는 방향으로 물체를 바라봤을 때의 이미지를 render할 수 있다는 것이죠.
결국 다양한 각도에서 촬영된 이미지를 갖고 NeRF를 학습시킨 후, 중간 각도에서 바라본 새로운 이미지를 만들어낼 수 있는 것이죠.
자세히 말하면, NeRF모델을 학습시키기 위해 우리가 필요로 하는 것은 (1) 특정 장면(scene)에 대해 같은 시간 다양한 각도에서 촬영한 2D 이미지들과 (2) 카메라 파라미터(카메라의 위치와 방향 및 초점거리 등의 정보) 입니다. 학습된 NeRF를 통해 알아낼 수 있는 정보는 (1) 3차원 장면 내 특정 입자의 color와 density , 그리고, 직선상의 입자들을 종합하여 계산해낼 수 있는 (2) 특정 viewing direction에서 render된 pixel의 색상 입니다.
NeRF MLP의 input과 output
NeRF 딥레닝 네트워크의 input과 output을 알아봅시다. 정보를 알고싶은 한 3차원 좌표(3d coordinate)와 바라보는 방향(viewing direction)을 집어넣으면 해당 입자의 color와 density값을 얻을 수 있습니다.
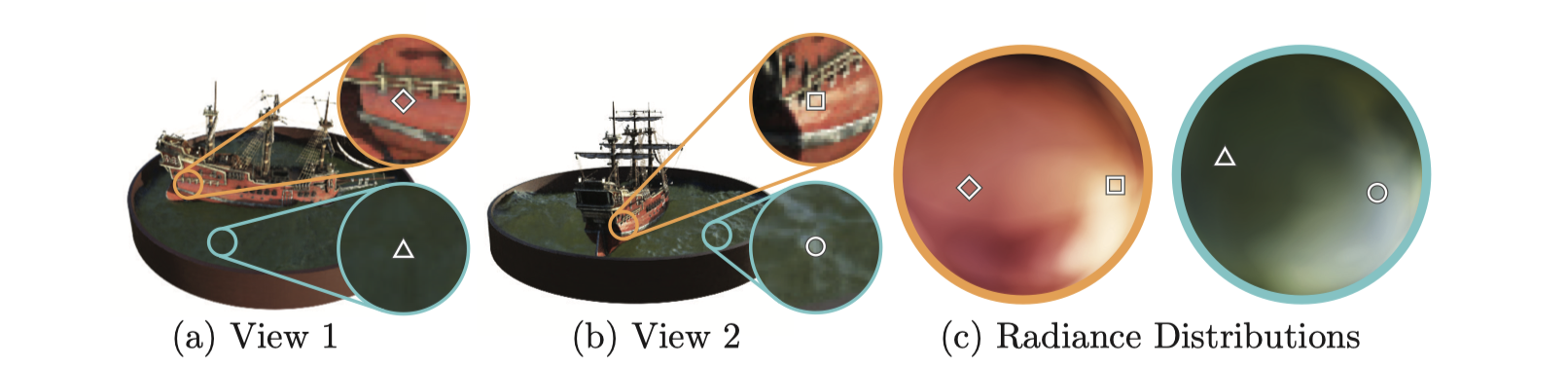
여기서 주목할 부분이 있습니다. NeRF에서는 같은 위치의 입자라도 바라보는 방향에 따라 다른 색상값을 출력한다는 것입니다! (사진5)는 같은 장면을 View1와 View2에서 바라본 모습을 각각 나타냅니다. 같은 위치의 입자더라도 View1과 View2에서 빛의 반사에 따라 다른 색상을 가집니다. NeRF에서는 viewing direction도 입력값으로 받음으로써 이러한 성질을 반영하기 때문에 더 정확한 이미지를 출력할 수 있습니다.
NeRF의 활용
NeRF가 실제로 어떤 분야에서 어떻게 활용될 수 있을까요?

◾️ 가상현실(VR)과 증강현실(AR): NeRF를 통해 실사 기반의 고품질 3D 컨텐츠를 만들어낼 수 있습니다.
◾️ 영화 및 게임 산업: 현실 세계에 대한 3D 모델을 생성하기 때문에, 영화 및 게임 컨텐츠의 배경을 만드는데 도움이 될 수 있어요.
◾️ 실내 인테리어: 특정 공간을 NeRF모델로서 표현함으로써, 가구 배치나 실내 디자인을 설계하는데 도움이 될 수 있고, 부동산 거래시에도 참고될 수 있습니다.
◾️ 의학: 내시경 혹은 CT, MRI등을 통해 촬영된 이미지를 사용해 NeRF를 학습시킴으로써, 신체 내부의 모습에 대해 3D 모델링 할 수 있습니다. 수술 또는 의료 교육 등에 활용할 수 있어요.
◾️ 자율주행 자동차 또는 로보틱스: NeRF를 통해 현실 세계에 대한 3D 모델을 생성하여 자율주행 시스템에게 제공함으로써, 더 정확하고 효율적인 경로 선택에 도움을 줄 수 있습니다.
이처럼 NeRF는 다양한 곳에서 응용될 수 있습니다. 이제 NeRF기술을 이해해보고 싶은 마음이 충분히 생기셨을 것 같으니, 다음 단원부터 본격적으로 원리 설명을 시작하겠습니다.
II. 본론1
-
<본론1>에서는, NeRF의 모든 내용을 자세히 알아보기 전 큰 그림을 전체적으로 이해해보는 시간을 가져보겠습니다.
3. Ray와 Volume Rendering 개요
어떻게 NeRF의 MLP으로부터 우리가 원하는 시점(view)에서의 이미지를 렌더링(rendering)할 수 있을지 알아봅시다.
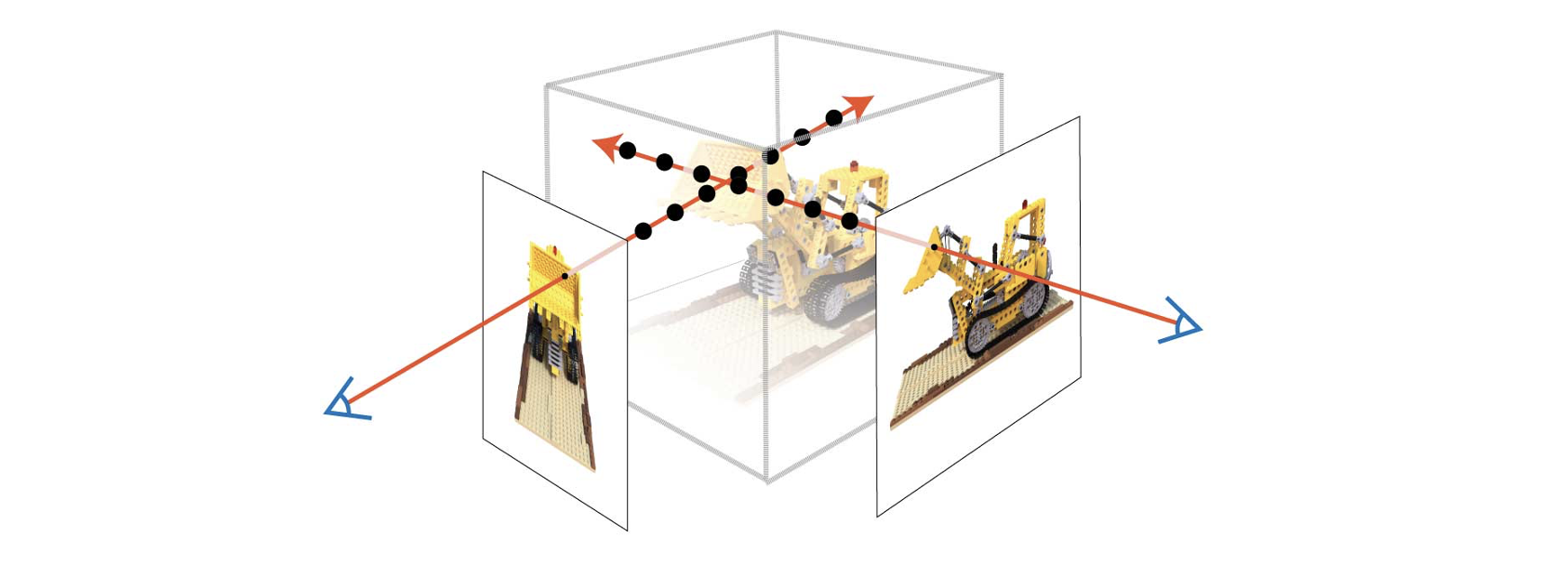
NeRF의 MLP는 3D 공간 상의 입자(3D particle)들의 정보를 담고 있습니다. NeRF에게 3D 공간상의 특정 점의 좌표 및 바라보는 방향을 input으로 주면 NeRF는 해당 3D particle의 색상과 밀도 정보를 출력합니다.
하지만 우리가 원하는 것은 3D 입자 하나하나의 값이 아니라 바라보는 시점(view)에서의 이미지이기 때문에, 이미지를 구성하는 모든 픽셀들의 색상값(RGB)을 계산해야 하죠. 각 픽셀의 색상값은, 해당 픽셀로부터 직선을 그어 그 직선을 구성하는 particle들의 정보를 통해 계산합니다. 이 때 사용되는 직선을 ‘ray’라고 합니다.
요약하자면, rendering 되는 픽셀 값은 그 픽셀에서부터 viewing direction방향으로 진행되는 ray상에 있는 모든 particle들의 색상, 밀도값을 종합하여 계산됩니다.
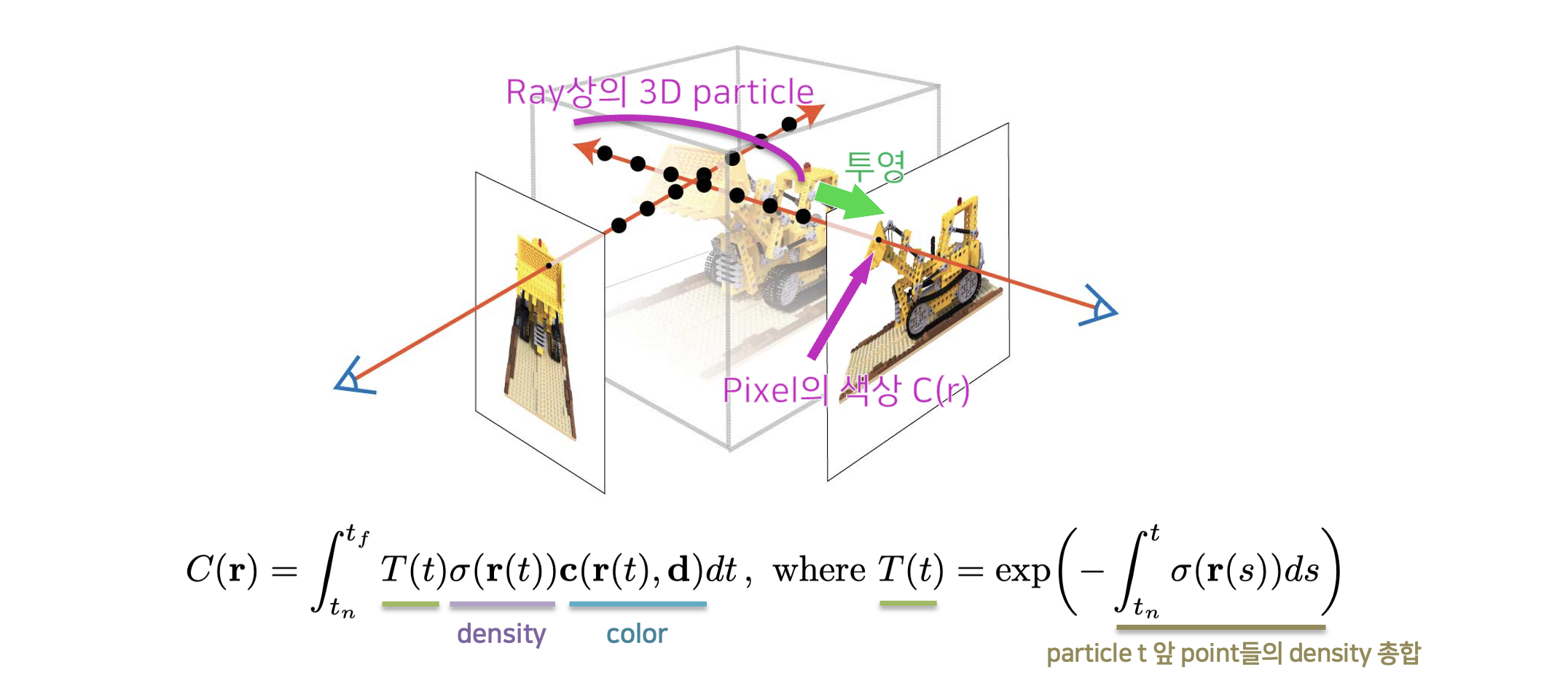
NeRF에서는 volume rendering을 통해 3차원 공간의 ray상의 점들을 적분하여 2차원상의 픽셀의 색상을 결정합니다. (이때 주의할 것은, 현실적으로 연속적인 모든 점을 적분할 수 없으므로, ray상의 일부 particle들을 샘플링 하여 더한다는 것입니다.) 투과된 픽셀의 색상을 알기 위해서는 R, G, B 각각 ray상의 particle들의 색상을 더하여 얻을 수 있습니다. 이 때, density가 높은 particle은 더 많은 비중을 두고 density가 낮은 particle들은 더 낮은 비중을 주어 더하죠. 이 뿐만 아닙니다. 특정 particle 앞에 많은 particle이 가로막고 있다면 렌더링 했을 때의 해당 particle의 영향력은 감소할 수 밖에 없습니다. 따라서 픽셀 앞에 있는 particle들의 density들을 종합하여 ‘누적된 투과율’ 이라는 것을 추가적으로 곱해 줍니다.
지금까지 ray의 volume rendering을 통해 렌더링된 이미지 내 픽셀 하나 하나의 색상값을 계산해내는 대략적인 과정을 알아보았습니다. 수식을 비롯한 더 자세한 내용은 hierarchical volume sampling을 배운 후 8단원 에서 이어서 설명드리도록 하겠습니다.
4. NeRF 학습 과정 정리
이번 단원에서는 NeRF 모델을 학습시키는 단계들에 대해 대략적으로 설명한 후, 다음 단원에서부터 각 단계에 대해 자세히 알아보도록 하겠습니다.
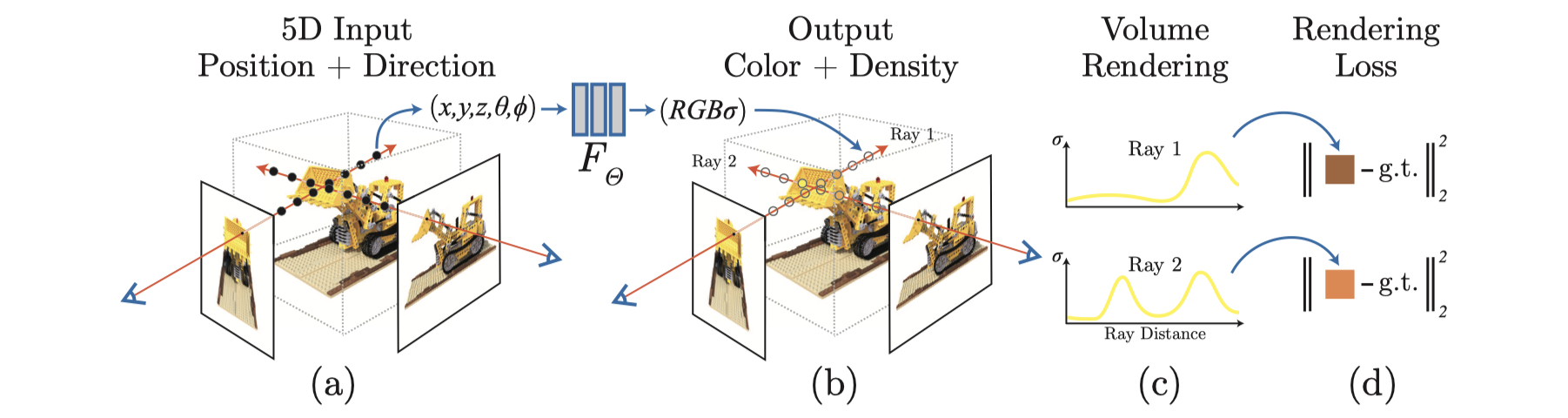
1단계. 샘플 이미지 기반으로 ray 구성하기
학습 데이터로 제공된 이미지들의 모든 픽셀 집합 중 특정 픽셀을 선택하고, 그 픽셀로부터 scene 방향으로 출발하는 ray를 $ r(t) = o + td $ 로 구성합니다.
2단계. Ray상에서 point들을 샘플링하기
ray상의 near bound와 far bound 범위 사이에서 $ N $ 개의 point를 샘플링 합니다. (사실 ray 전체에 걸쳐 샘플링 된 후 물체가 있는 부분에 대해 집중적으로 한번 더 샘플링 합니다. 자세한 설명은 5단원을 참고해주세요.)
3단계. 샘플링된 모든 점에 대해 각각 MLP에 query하기
샘플링된 $ N $개의 point들 각각을 MLP에 input값으로 대입합니다. MLP로부터 각 point들의 color와 density값을 얻습니다.
4단계. Volume rendering을 통해 예측된 색상값 계산하기
Ray의 각 point별 color, density값을 가지고 고유의 색상값을 계산해 냅니다. 이 값은 ray에 대한 MLP의 예측값입니다. (자세한 설명은 8단원을 참고해주세요.) Volume rendering 과정은 미분가능하기 때문에 loss에 대한 gradient를 계산하는데 방해가 되지 않습니다.
5단계. Loss 계산하기
4단계에서 구한 예측값과 샘플 이미지의 실제 색상값(ground truth) 사이의 오차(loss)를 구합니다. Loss로는 squared error를 사용합니다. (자세한 설명은 9단원을 참고해주세요.)
6단계. Back-propagation
MLP 내 각 파라미터당 loss의 변화율(gradient)을 계산한 후 gradient descent를 실시하여 optimize를 해나갑니다. 1~6단계가 iteration 횟수만큼 반복됩니다.
III. 본론2
- <본론2>에서는, NeRF의 학습 중 수행되는 세부 과정들에 대해 자세히 알아보도록 하겠습니다.
5. Hierarchical Volume Sampling
개요
4단원의 2단계에서 소개된, 학습시 input으로 사용할 point들을 샘플링하는 과정에 대한 설명입니다.
NeRF에서 적절한 샘플링 포인트를 선택하는 것은 중요합니다. 너무 많은 point들을 선택하면 계산 비용이 많이 들기에 실제로 물체가 존재하는(즉, 더 많은 정보를 표현하고 있는) point들을 집중적으로 선택하는 것이 더 효율적이죠. 따라서 NeRF에서는 성능을 향상시키기 위해 point들을 샘플링 할 때 ray 전체에 걸쳐 고르게 sampling하는 것이 아니라 밀도가 높은 영역에서 더 많이 샘플링 하는 Hierarchical volume sampling이 이루어집니다.
Hierarchical volume sampling은 전체 ray에서 균등하게 샘플링된 점으로 먼저 예측 색상을 계산하고(coarse network), 이 중에서 밀도 가 높은 점들을 집중적으로 샘플링하여 최종 예측 색상을 계산하는 과정(fine network) 입니다.

Hierarchical volume sampling 수행 과정
Hierarchical volume sampling의 과정은 다음과 같습니다. $ N_c $(coarse network 의 샘플링할 point의 수) 와 $ N_f $(fine network를 위해 샘플링할 point의 수) 는 hyperparameter이며, 논문에서는 $ N_c = 64, N_f = 128 $ 을 채택하였습니다.
(1) Ray를 $ N_c $ 개의 구역으로 나누고, 각 구역에서 point를 하나씩 선택합니다. (Startified sampling)
(2) 이 $ N_c $ 개의 point들을 MLP에 집어넣어 $ N_c $ 개의 color, density 아웃풋을 얻고, 이를 종합하여 ray의 예측 색상 $ \hat{C}_c(r) $ 을 계산합니다. 아래 첨자 $ c $ 는 coarse network의 color 예측값임을 의미합니다.
\[\hat{C}_c(r) = \sum\limits_{i=1}^{N_c}{w_i c_i} \quad , \quad w_i = T_i(1 - exp(-\sigma_i \delta_i))\]위 수식은 coarse network의 color를 계산하는 수식입니다(volume sampling 이용). 수식은 ray를 $ i $개의 구간으로 나누어 구간당 point를 하나씩 할당하고, $ i $ 개의 point에 대한 color $ c_i $ 와 weight $ w_i $ 를 곱하여 가중치합을 구한 것을 의미합니다. 이 수식에서 weight $ w_i $ 는 해당 point가 ray상에서 얼마나 영향력을 갖는지를 의미합니다. 그 point의 density인 $ \delta_i $ 가 높을수록 $ w_i $ 값이 커짐을 알 수 있습니다.
(3) 각 particle의 weight값들을 아래와 같은 수식을 통해 normalize합니다. Normalize 결과, 모든 weight의 합은 1이 됩니다. 따라서 각 weight ($ w_i $)를 해당 point $ i $ 에 대응하는 확률로 생각할 수 있습니다.
\[\hat{w}_i = {w_i \over \sum\limits_{j=1}^{N_c}{w_j}}\](4) 확률분포에 따라 ray상에서 $ N_f $ 개의 점을 추가적으로 샘플링합니다. 이 때 밀도가 높은 point들, 즉, 물체가 있는 공간의 point들이 주로 샘플링됩니다.
(5) 최종적으로 $ N_c + N_f $ 개의 point를 모두 fine network에 입력하여 각 point의 color & density를 얻은 후, volume rendering을 사용하여 최종적인 color 예측값을 산출합니다.
샘플링 알고리즘: Inverse Transform Sampling
확률변수가 ray상의 point이고 (확률값이 weight인) 확률밀도함수(PDF)가 주어졌다고 했을 때, 위에 설명된 weight들의 확률분포에 따라 임의의 point들을 선택하고 싶은 상황입니다.
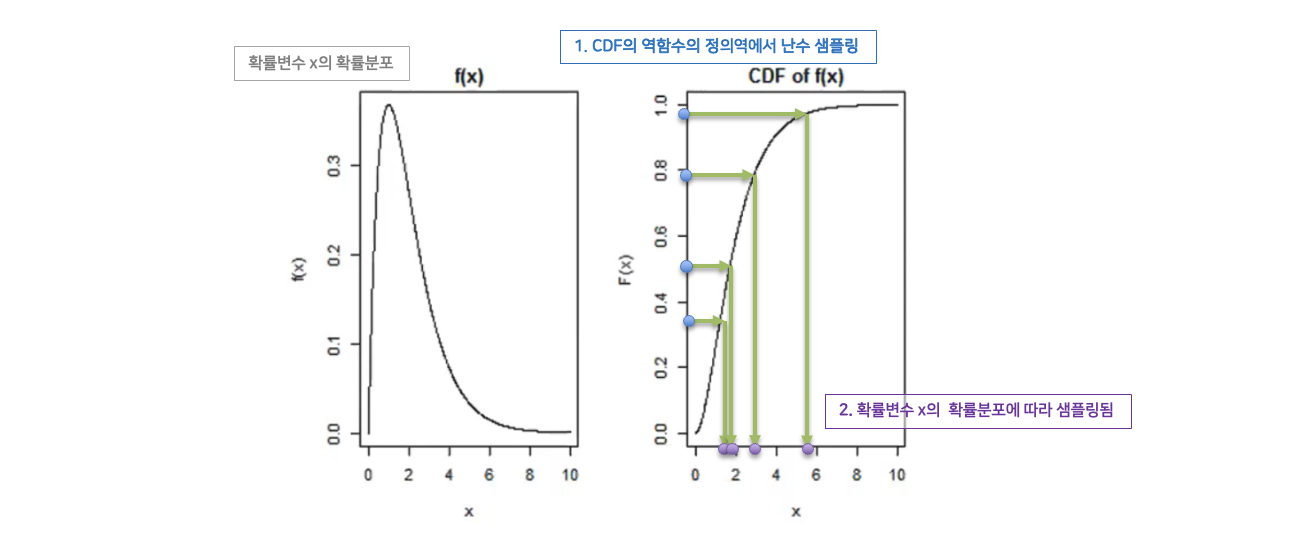
이때 PDF를 적분하여, 확률변수가 특정 값 이하가 될 확률분포를 나타내는 CDF(Cumulative distribution function) 를 구할 수 있습니다. 이 때 CDF의 함숫값은 [0,1] 범위에서 균일 분포(uniform distribution)를 갖습니다. 여기서 CDF의 함숫값을 난수에 따라 샘플링하고 이에 대응하는 x값을 선택하면, (즉, CDF의 역함수에서 [0,1] 사이의 특정 확률 분포를 따르는 x값에 대응하는 함숫값을 선택하면,) x값을 ‘처음 x의 확률분포에 따라서’ 샘플링한 값이 됩니다. 이는 “연속적인 $ X $에 대한 CDF $ Y=F(X) $ 에 대해 $ Y $는 균일 분포를 따른다”는 성질 때문입니다. 이 과정을 inverse transform sampling이라고 하고, 더 알아보고 싶으면 위키피디아를 참고해 주세요.
이처럼 Inverse transform sampling을 사용하면 주어진 화률 분포에서 난수를 생성할 수 있고, 결과적으로 coarse network에서 구한 밀도 분포에 따라 fine network의 입력 point들을 비례적으로 샘플링 할 수 있습니다. 즉, 더 밀도가 높아 더 영향을 많이 주는 point들을 더 많이 샘플링 할 수 있다는 것입니다.
6. Positional Encoding
NeRF의 MLP에 점의 위치($ x, y, z $)와 바라보는 각도($ θ, φ $)을 단순히 그냥 입력하는 것이 아니라 positional encoding 을 적용시켜 더 고차원의 벡터로 변화시켜 입력합니다. Positional encoding을 적용하는 이유는 MLP가 더 정밀하고 복잡한 고주파의 (high frequency) 정보를 표현하기 위해서 입니다. 이것이 어떤 의미인지 알기 위해 아래 사진을 바라봅시다.

(사진12)의 오른쪽 그림은 왼쪽 그림에 비해 사자의 모습이 더 선명하게 나타납니다. 따라서 오른쪽 그림을 표현하는 neural network가 positional encoding을 적용하였기 때문에 고주파의 정보를 더 담고 있다고 할 수 있죠.
Rahaman et al 의 논문에 따르면, deep neural network가 저주파 성분에 편향적으로 학습되는 경향이 있다고 합니다. 이를 극복하여 고주파의 정보를 담기 위해, NeRF에서는 MLP에 input으로 대입하는 정보(좌표, 방향)를 더 고차원의 벡터로 변환시켜 대입합니다.
NeRF의 positional encoding 수식은 아래와 같습니다.
\[\gamma(p) = (sin(2^0 \pi p),\,cos(2^0 \pi p),\,sin(2^1 \pi p),\,cos(2^1 \pi p), \,...\,, sin(2^{L-1} \pi p),\,cos(2^{L-1} \pi p))\]이 수식에 대입하기에 앞서, viewing direction $ θ, φ $(2차원)을 데카르트 좌표계 기준의 3차원 벡터로 변환합니다. 이후 location과 viewing direction을 $ [-1, 1] $ 범위로 normalize 합니다. 그런 다음, 점의 location($ x, y, z $) 및 viewing direction을 각각 위 수식의 $ p $에 대입하여 증폭된 벡터($ 2L $ 차원)를 얻습니다. 총 3개의 위치 정보와 3개의 방향 정보가 각각 위 수식과 같은 positional encoding 과정이 적용되는 것입니다.
논문에서 location 정보에 대해서는 $ L $ 값을 10으로 채택하였고, viewing direction 정보에 대해서는 $ L $ 값을 4로 지정했습니다. 지금까지 설명한 것을 토대로, location정보는 3차원에서 60차원이 되며 (3$ \times $ (10$ \times $2)), viewing direction 정보는 2차원에서 3차원으로 변환된 후 24차원이 됨(3$ \times $(4$ \times $2))을 알 수 있습니다.
이렇게 input을 고차원으로 만듦으로써 positon이나 direction 변화에도 input값에 있어 큰 변화가 되기 때문에 더 미세한 정보를 MLP에 담을 수 있는 효과가 있으며, 결국 scene 내부의 세부적인 구조와 질감을 표현하는 데 도움이 됩니다.
7. MLP Structure
이번 단원에서는 NeRF의 neural network의 구조, batch size, optimization 알고리즘 등에 대해 설명하겠습니다.
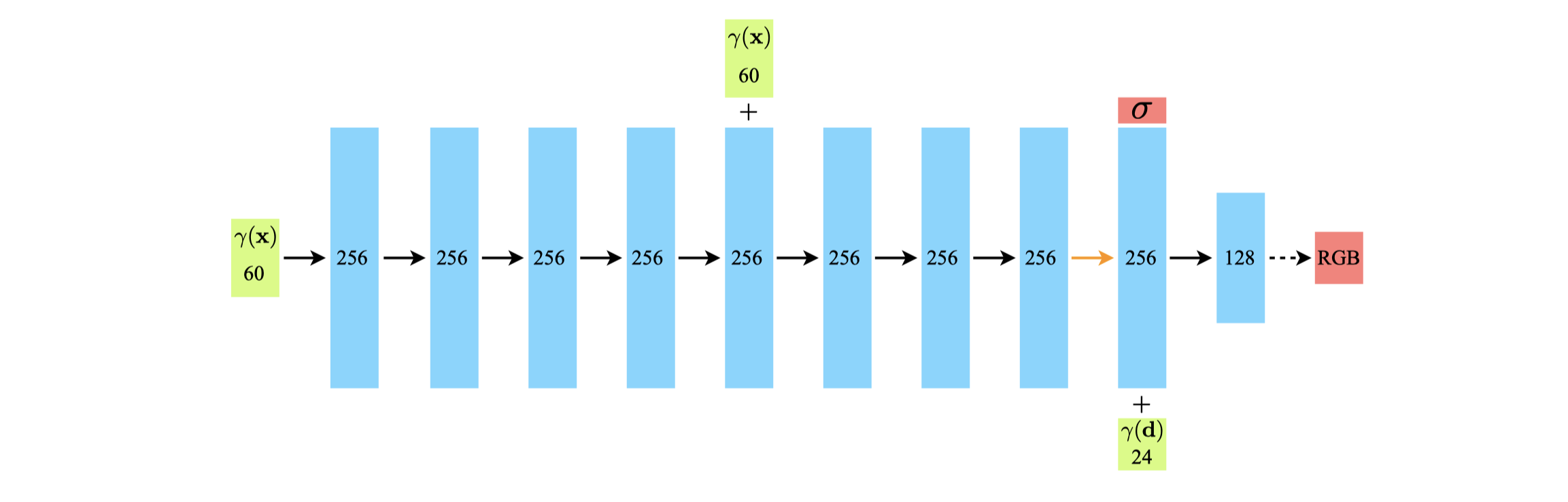
위 그림은 NeRF에서 사용된 MLP의 구조를 나타냅니다. 파란색 상자는 hidden layer를 표현하며, 초록색 상자는 input을, 빨간색 상자는 output을 표현합니다. $ \gamma $는 positional encoding 함수를 나타냅니다. 또한 검정색 실선 화살표는 ReLU activation을, 검정색 점선 화살표는 sigmoid activation을, 주황색 화살표는 activation이 없음을 나타냅니다.
주목할 포인트는 3D point의 위치($ x $), 방향($ d $) 벡터가 MLP에 입력되는 타이밍과, 색상(RGB)와 밀도($ \sigma $)벡터의 출력 타이밍입니다. Location($ x $)만 갖고 layer를 투과하여 density($ \sigma $)가 예측되며, density가 출력될 때 direction($ d $) 정보까지 추가적으로 입력되어 색상(RGB) 이 예측됩니다. 이는 2단원에서 설명한 NeRF의 “density는 점의 위치에 따라 결정되고 color는 점의 위치와 바라보는 방향에 따라 결정된다”는 성질을 반영하고 있습니다.
Layer당 unit 수는 마지막 layer를 제외하고 256개이며, DeepSDF 아키텍처를 따르기 때문에 5번째 hidden layer에서 skip connection을 위해 한번 더 위치 벡터($ x $)을 대입합니다 (exploding gradient problem 해결을 위해서).
4096개의 ray가 하나의 batch를 이룹니다. Ray상에서 샘플링은 5단원에서 배웠던 hierarchical volume sampling을 사용하며 coarse network를 위해 64개의 point를($ N_c = 64 $), fine network를 위해 128개를 추가적으로 샘플링하여 192개의 point를 사용합니다($ N_f = 128 $). 따라서 한 ray당 256번의 query가 일어난다고 할 수 있습니다.
Optimizing 알고리즘으로는 adam optimizer를 사용하며($ \beta_1 = 0.9, \beta_2 = 0.999 $), learning rate 를 $ 5 \times 10^{-4} $ 에서 $ 5 \times 10^{-5} $ 으로 decay합니다. Iteration 횟수는 일반적으로 10만회에서 30만회 정도 수행합니다.
8. NeRF Volume Rendering
5단원에서는 한 ray에서 여러 point를 샘플링하는 방법에 대해 배웠고, 3단원에서는 point들의 MLP 아웃풋들을 volume rendering하여 ray의 예측 색상값을 구한다는 것도 알아보았습니다.
이번 단원에서는 volume rendering과정을 더 구체적으로 공식화하여 알아보도록 하겠습니다.
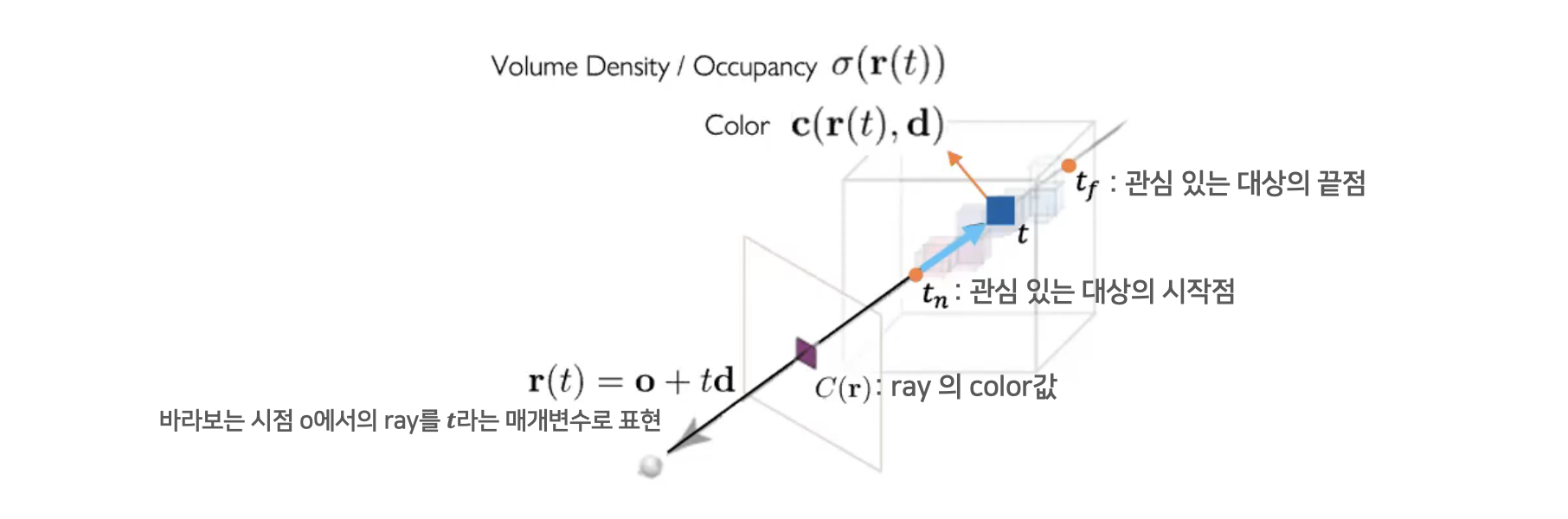
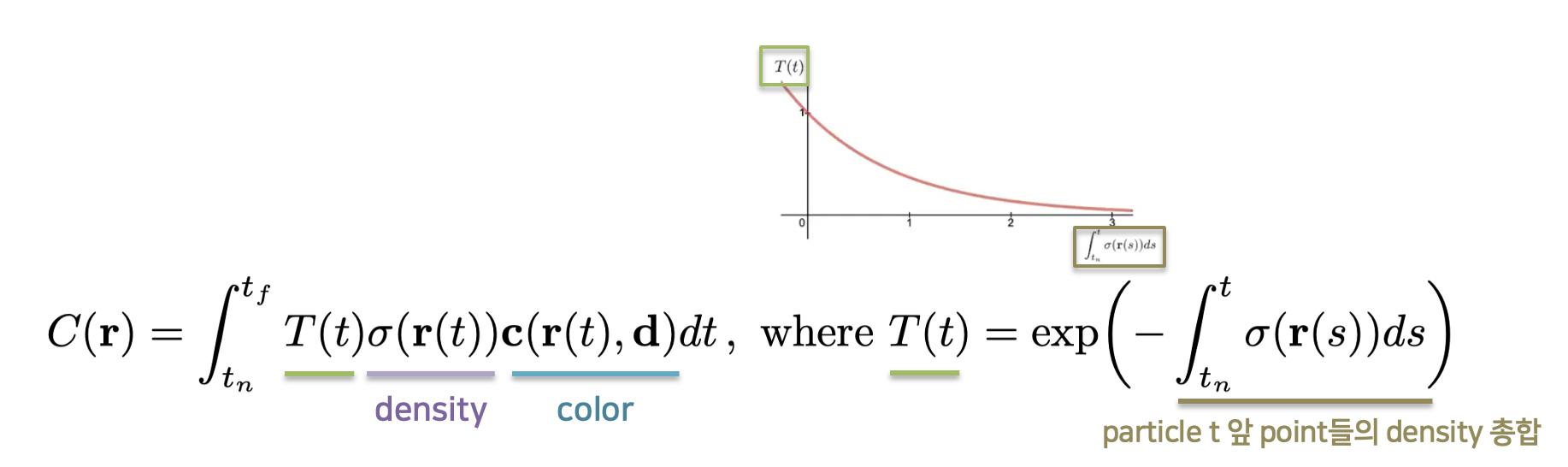
위 수식은 ray의 $ t_n $ 지점부터 $ t_f $ 지점까지의 연속적인 점들에 대한 color를 구하는 volume rendering 수식입니다. (사진14)에서 볼 수 있듯이, $ t_n $은 rendering 대상의 시작점(near bound)을 의미하고 $ t_f $ 는 rendering 대상의 끝점(far bound)을 의미합니다.
Volume rendering은 $ t_n $ 과 $ t_f $ 사이 구간에서, 각 $ t $ 에 대한 “위치($ r(t) $)와 보는 방향($ d $)에 대한 color값”, “보는 방향($ d $)에 대한 density값”, 그리고 “$ T(t) $” 를 연속적으로 더하는(적분하는) 것임을 확인할 수 있습니다.
그렇다면 $ T(t) $ 가 의미하는 것은 무엇일까요? 수식의 오른쪽 부분을 보면, $ T(t) $ 는 $ t_n $(시작점) 에서 $ t $ 까지 density들을 적분한 후, 그것을 $ y = e^{-x} $ 에 대입한 것이라고 되어 있습니다. $ y = e^{-x} $ 그래프의 증감 방향을 고려할 때, density들을 적분한 값이 작아질 수록 $ T(t) $ 의 값은 커짐을 알 수 있습니다. 즉, 해당 point 앞을 가로막고 있는 point들의 밀도가 작을 수록 해당 point가 큰 비중을 갖는다고 해석할 수 있죠. 앞에 뭔가가 없을수록 뒤에 있는 것이 잘 보인다는 자연적인 원리를 생각해 볼 때 매우 합리적인 과정이라고 할 수 있습니다.
하지만, NeRF에서는 현실적으로 연속적인 모든 점들에 대한 color, density, $ T(t) $ 를 계산하기 힘듭니다. 5단원 에서 배운 대로 일정 개수만큼의 점을 샘플링하기 때문에, 위 classic volume sampling 근사한 아래 volume rendering을 사용합니다.
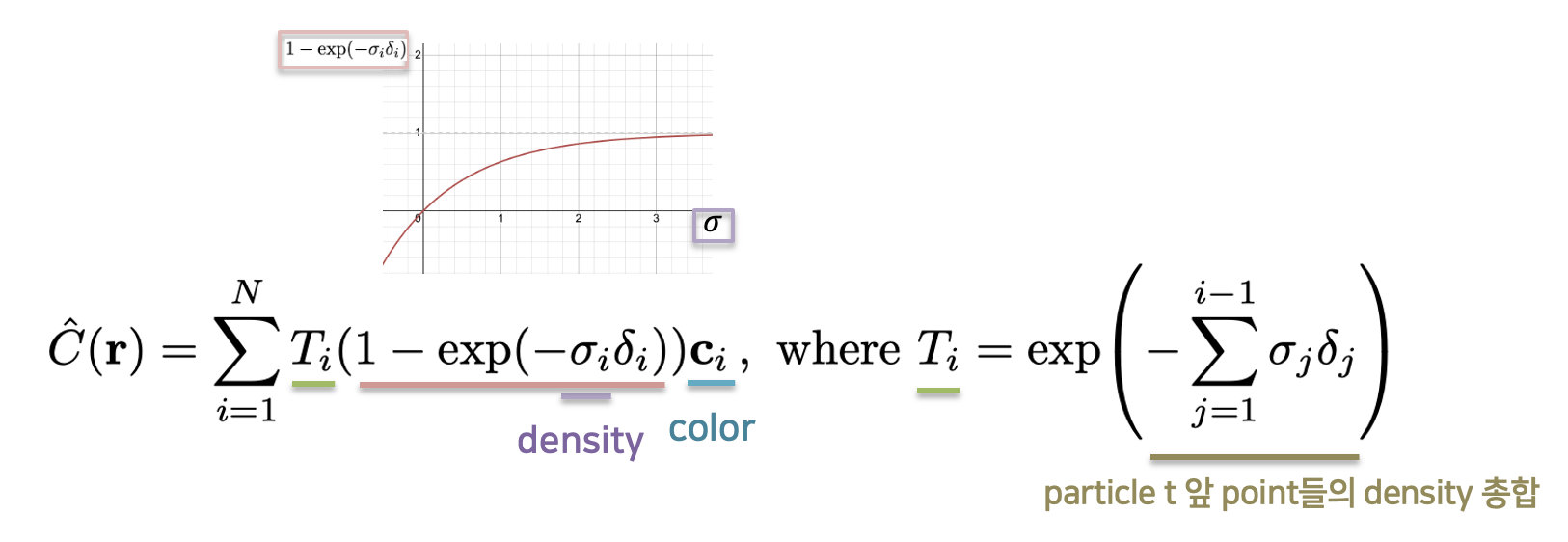
NeRF에서는 이산적으로 샘플링 된 점에 대해 volume rendering을 수행하지만, 적분($ \int $)이 합계 ($ \sum $)으로 바뀌었을 뿐, 각 구성 요소가 의미하는 것은 크게 다르지 않습니다.
5단원에서 배운 coarse network와 fine network를 위해 샘플링된 점들 ($ N_c $ 또는 $ N_f $)이 있습니다. $ N_c $ 또는 $ N_c + N_f $ 만큼 반복하며 color, density, $ T $값을 곱하여 더해줍니다 ($ T $ 의 의미에 대해서는 두 단락 이전 내용 참고할 것).
이 때, density($ \delta $) 가 그냥 대입되는 것이 아니라 $ 1 - e^{-\sigma_i \delta_i} $ 함수가 적용되어 대입되는 것이 특징입니다. density가 커질 수록 큰 값을 갖지만, 1을 넘지는 않게 함으로써 이산적인 확률변수의 확률값의 특징을 갖도록 하였습니다. 그래프를 토대로 density가 커질수록 해당 함수의 함숫값도 커짐을 확인할 수 있습니다. $ \delta_i $ 샘플링된 점 사이의 간격을 의미합니다 ($ \delta_i = t_{i+1} - t_{i}$).
9. Loss Computation
모델을 optimize하기 위해서는 예측값의 실제 ground truth값과의 오차를 계산하는 loss computation 과정이 필요합니다.
Ground truth는 우리가 입력한 이미지들의 픽셀의 color값 입니다. 이 픽셀에 대응하는 하나의 ray에 대해 query한 점들의 color와 density를 기반으로 volume rendering 하면 예측한 color 값을 얻을 수 있습니다. 이 둘의 차의 L2 norm을 통해 rendering loss를 구합니다. 수식은 아래와 같습니다.
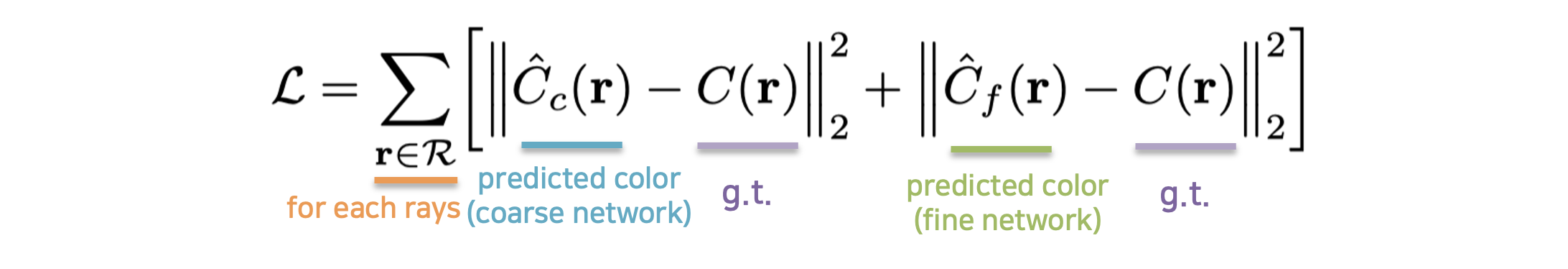
일정 간격으로 샘플링한 $ N_c $ 개의 샘플을 coarse network에 대입하여 얻은 출력값을 volume rendering 하여 $ \hat{C}_c(r) $ 값을 얻습니다. 그리고 밀도가 높은 곳에서 샘플링 빈도를 높인 $ N_c + N_f $ 개의 샘플을 fine network에 대입하여 얻은 출력값을 volume rendering 하여 $ \hat{C}_f(r) $ 값을 얻습니다. 이 둘의 loss를 더하여 한 ray에 대한 loss를 계산할 수 있죠. (Sampling에 대한 자세한 설명은 5단원을 참고해 주세요.)
Batch에 담긴 ray의 수만큼 이 과정을 반복하여 전부 더하여 batch에 대한 cost를 얻습니다. 이 cost를 얻은 후, 이를 기반으로 gradient를 계산하여 back-propagation을 실시합니다. 이것까지가 한 iteration이라고 할 수 있습니다. Volume rendering 공식이 미분 가능하기에 편리하게 최적화할 수 있습니다.
논문에서는 ablation study를 통해 batch size를 4096개의 ray로 채택했으며, $ N_c $는 64, $ N_f $ 는 128을 채택했습니다.
결과적으로 3차원 물체를 학습시키기 위해 필요한 것은 3차원 데이터가 아닌, 2차원 이미지 (color map)과 카메라 파라미터(카메라의 위치, rotation등의 정보) 뿐입니다. 필자가 실험을 해본 결과, 개인적으로 찍은 사진들을 갖고도 colmap 프로그램을 통해 카메라 파라미터를 계산한다면 바로 NeRF 모델을 학습시킬 수 있었습니다. 이러한 단순성이 NeRF의 큰 장점 중 하나라고 생각합니다.
IV. 결론
- NeRF가 다른 모델과 비교해서 가지는 이점이 무엇인지, 단점과 개선 방향은 어떤 것이 있는지에 대해 설명하겠습니다.
10. 성능 비교
논문에서는 NeRF모델을 SRN, NV, LLFF와 비교하였습니다.
- SRN(Scene Representation Networks)는 불투명한 표면의 데이터를 표현하는 모델로써, 특정 좌표의 feature vector를 예측하는 부분, feature vector으로부터 색상을 예측하는 부분으로 나뉩니다.
- NV(Neural Volume)는 복셀 그리드(voxel grid)를 재구성하는 모델로써 배경과 객체가 따로 주어져야 한다는 특징이 있습니다.
- LLFF(Local Light Field Fusion)는 실사 기반의 뷰 생성을 위한 모델로써, 3D CNN을 사용하여 불연속적인 RGB grid를 예측합니다.
그리고 뷰를 합성한 결과를 ground truth와 비교할 때 사용한 평가 지표로는 PSNR, SSIM, LPIPS를 사용했습니다.
- PSNR: 최대 신호에서의 잡음 비율로써, 대조군에 대한 화질 손실의 정도를 평가합니다. 값이 높을수록 좋습니다.
- SSIM: 두 의미지의 유사도를 다양한 요소를 통해 분석합니다. 값이 높을수록 좋습니다.
- LPIPS: 딥러닝 네트워크를 사용하여 high level feature를 추출하여 유사도를 평가합니다. 값이 낮을수록 좋습니다.

3D 객체를 나타내는 “Diffuse Synthetic 360 데이터”와 “Realistic Synthetic 360” 데이터에 대해서는 NeRF가 다른 모델과 비교했을때 모든 지표상에서 뛰어난 결과를 나타냈고, 실사 기반의 Real Forward Facing 데이터에 대해서는 LPIPS 지표를 제외하고 뛰어난 결과를 나타냈습니다.

주관적 화질 비교 결과 NeRF가 섬세한 디테일을 대체로 잘 표현하며 경계선을 더 안정적으로 나타내는 것으로 확인되었습니다. 그럼에도 불구하고, 빛 반사에 대해서는 개선이 필요한 부분이 보입니다.
11. 결론 및 개선점
NeRF는 복잡한 실사 데이터를 MLP상의 weight를 통해서 적은 크기로 표현할 수 있다는 점과, 깊이 및 3D 정보가 필요하지 않다는 점, 그리고 렌더링 과정이 미분 가능하기 때문에 gradient 기반 optimization을 사용할 수 있다는 점으로 인해 매우 혁신적인 모델로 평가받고 있습니다.
하지만 다음과 같은 단점이 존재합니다.
- 학습 시간이 매우 느립니다. 한 장면을 정밀하게 표현하기 위해 100,000만 회 이상의 iteration을 수행해야 하며, 이는 8시간 이상의 학습 시간을 요구합니다.
- 정적인 scene에 대해서만 표현이 가능합니다. 시간적으로 하나의 시점만 표현 가능하며, 움직이는 물체에 대한 표현이 불가합니다.
- 하나의 scene에 overfit 합니다. 특정 물체에 대해 학습한 모델은 해당 물체에 대한 view만 합성할 수 있습니다.
- 학습을 위해 사진들과 함께 카메라의 초점거리, 카메라의 위치, 카메라의 방향 등의 카메라 파라미터 정보가 필요합니다.
2020년 NeRF가 발표된 이후, 이러한 단점을 보완하기 위해 다양한 개량형이 나오고 있습니다. 이 사이트에는 NeRF를 응용한 모델에 대해 종류별로(faster training, generalization, video 등등) 잘 정리되어 있습니다.
NeRF 포스팅을 마치겠습니다. 읽어주셔서 감사합니다.😀
Reference
사진1
사진2(1)
사진2(2)
사진2(3)
사진4
사진5
사진6(1)
사진6(2)
사진6(3)
사진6(4)
사진7
사진9
사진10
사진11
사진13
사진14

댓글남기기