[Instant-NGP][이론] Instant Neural Graphics Primitives 개념 설명 및 논문 리뷰
들어가기에 앞서..
- 이 포스팅은 SIGGRAPH 2022에 수록된 “Instant Neural Graphics Primitives with a Multiresolution Hash Encoding” 논문을 바탕으로 작성되었습니다.
- Instant-NGP 프로젝트 페이지 링크: https://nvlabs.github.io/instant-ngp
- NeRF와 친숙하지 않으신 분들은 필자의 NeRF 포스팅을 미리 읽으시는 것을 추천드립니다.
- 단순히 논문을 순서대로 해석한 글이 아니라, 이해하기 쉬운 글이 되도록 순서를 재구성하였습니다. 용어는 원어의 사용을 지향하였습니다.
목차
순서대로 읽으시는 것을 권장드립니다!
- Instant-NGP 소개 👉바로가기
- NeRF와 positional encoding 👉바로가기
- Parametric Encoding 👉바로가기
- Dense & Sparse Parametric Encoding 👉바로가기
- Parametric Encoding in Instant-NGP 👉바로가기
- Multiresolution Hash Encoding 👉바로가기
- Hyperparameters 👉바로가기
- 구현상의 특징 👉바로가기
- 결과 비교 및 결론 👉바로가기
1. Instant-NGP 소개
NeRF에서는 인공 신경망(neural network) 안에 위치하는 ‘가중치’라는 파라미터들에 scene에 대한 모든 정보를 담았습니다. 그렇기 때문에 고차원의 feature 까지 담을 수 있는 매우 깊은 layer의 네트워크를 필요로 했죠.
하지만 Instant-NGP에서는 ‘표현’을 위해 neural network 만 쓰이지는 않습니다. Input data가 neural network 에 대입되기 전에 ‘학습될 수 있는 특정 자료구조’를 거치죠 (2단원 참고). 이러한 특징 덕분에 layer수가 감소하게 되며, 쿼리 속도와 학습 속도가 NeRF에 비해 획기적으로 단축될 수 있게 됩니다.
특히, Instant-NGP는 이 ‘학습될 수 있는 특정 자료구조’로 해시 테이블(hash table)을 사용합니다! 해시 테이블은 쿼리 속도가 매우 빠르다는 장점이 있죠. 이것 또한 Instant-NGP가 빠른 속도를 가질 수 있는 이유 중 하나입니다. 더불어, hyperparameter에 따라 해시 테이블의 크기를 원하는 대로 지정하므로써 예측 가능한 메모리 사용 구조를 만들어낼 수 있다는 장점도 있죠.

또한 Instant-NGP는 NVIDIA사에서 개발한 것으로써, CUDA 기반으로 짜여져 있기 때문에 GPU에 최적화된 코드를 포함합니다. 덕분에 NVIDIA GPU가 장착된 머신에서 더욱 빠른 연산속도를 제공합니다.
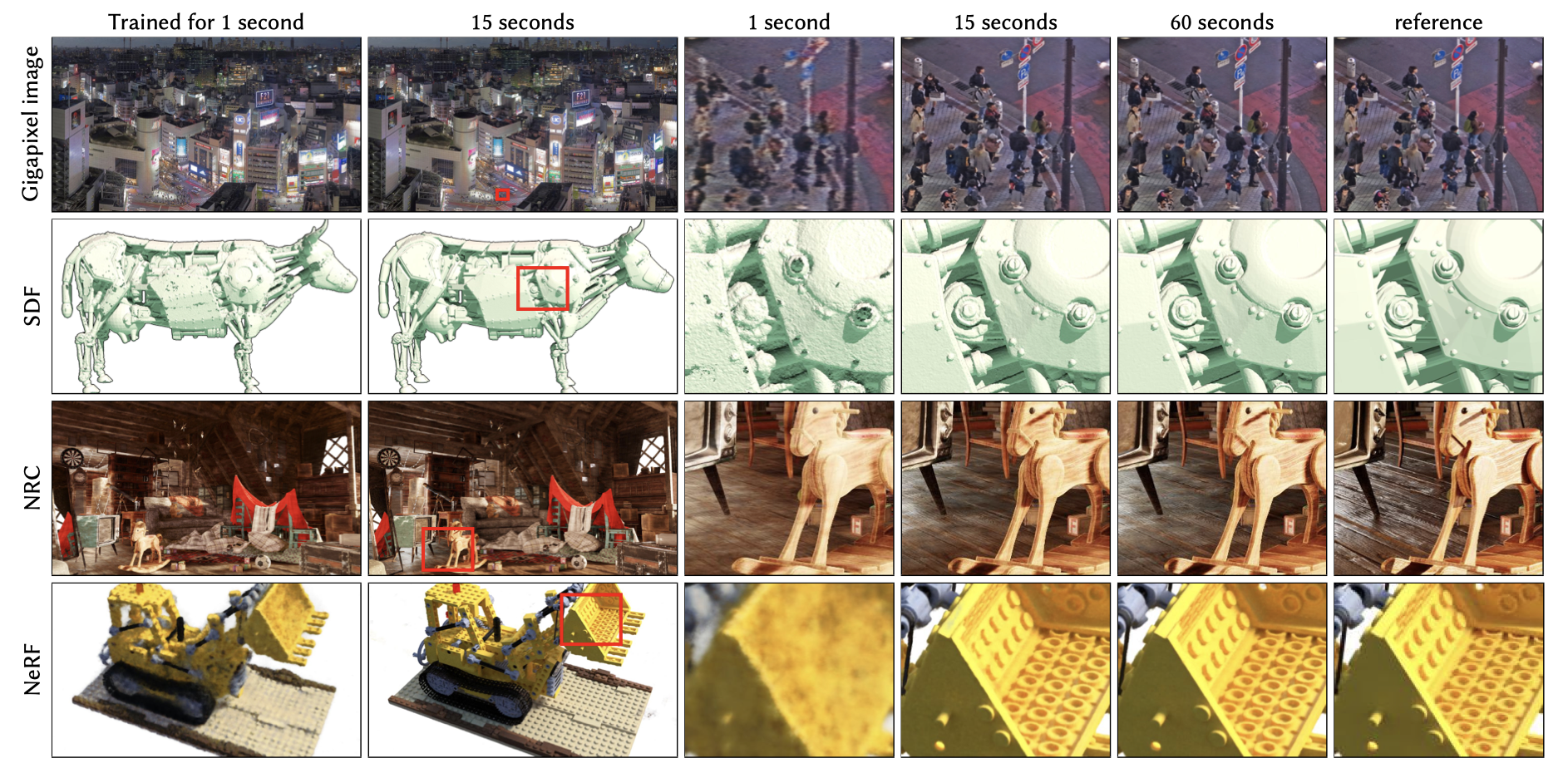
NeRF는 그동안 느린 연산 속도가 문제점으로 지적되어 왔는데, 위와 같은 세 가지 이유 덕분에 Instant-NGP는 매우 빠른 scene 학습이 가능하게 되었습니다.
또한, Instant-NGP는 NeRF 뿐만 아니라 Gigapixel image, SDF, NRC 등에도 적용이 가능합니다. 왜냐하면 multiresolution hash encoding을 neural network에 대입하기 이전에 적용시킨다는 Instant-NGP의 핵심 아이디어는 뒤에 어떤 neural network가 오던 상관없이 적용할 수 있기 때문입니다!
2. NeRF와 Positional Encoding
1단원에서 Instant-NGP가 4가지 task(gigapixel image, SDF, NRC, NeRF)에 적용될 수 있다고 설명했는데, 이제부터 이 4가지 중 NeRF에 적용하는 것을 중점적으로 보도록 하겠습니다.

NeRF에서 neural network에 3차원 점의 위치 정보($ x, y, z $), 바라보는 방향 정보($ θ, φ $)를 대입할 때 단순히 이 값들을 입력하지는 않습니다. Positional encoding을 거쳐서 더욱 더 고차원의 벡터로 변환 시킨 후 네트워크에 입력합니다. 이렇게 하는 이유는 좌표의 미세한 변화에도 많은 차이를 갖는 input값을 입력하여 neural network가 더 정밀하고 복잡한 정보를 표현할 수 있도록 하기 위함이었죠.
\[\gamma(p) = (sin(2^0 \pi p),\,cos(2^0 \pi p),\,sin(2^1 \pi p),\,cos(2^1 \pi p), \,...\,, sin(2^{L-1} \pi p),\,cos(2^{L-1} \pi p))\]NeRF의 positional encoding 수식은 위와 같습니다. 입력 좌표 (,방향)를 인코딩하는 것이 수식을 통해 이루어진다고 할 수 있습니다. 같은 좌표 또는 같은 방향에 대해서는 항상 같은 인코딩 결과를 만들어내죠. 수식으로 설명 가능한 numerical한 인코딩 과정이라는 것을 알 수 있죠.
반면, Instant-NGP에서는 parametric encoding이란 것이 쓰이는데, 인코딩 과정 마저도 “학습”이 존재한다고 보시면 됩니다. 다음 단원에서 설명이 이어지겠습니다.
3. Parametric Encoding
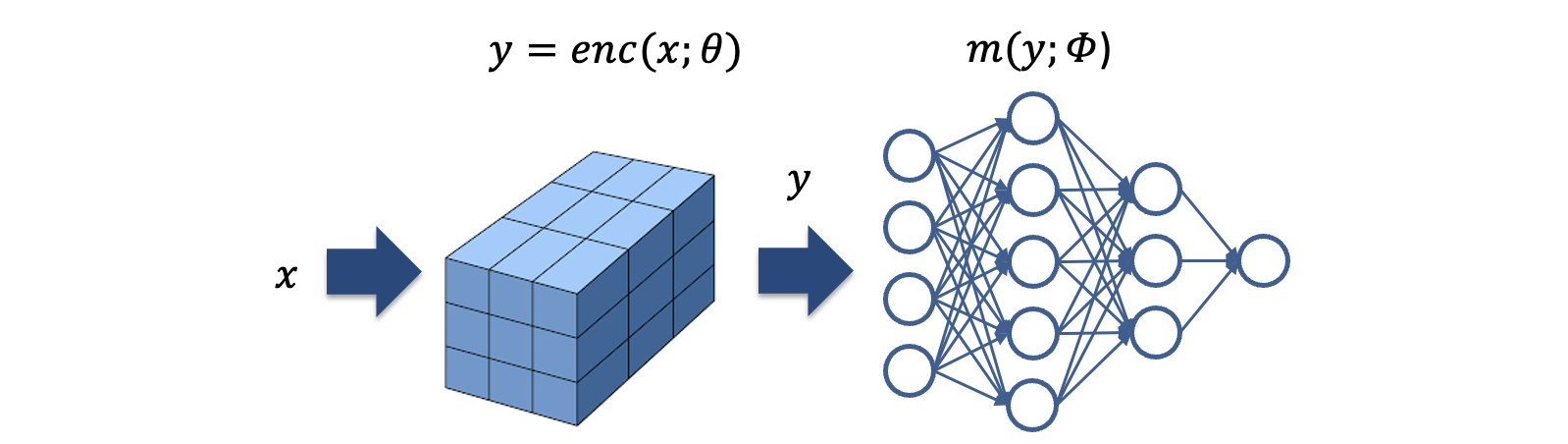
Parametric encoding은 기존의 MLP(multi layer perceptron) 안의 weight나 bias 뿐 아니라, neural network를 거치기 이전 단계에서도 학습 가능한(trainable) feature vector를 파라미터로 할당한다는 개념입니다.
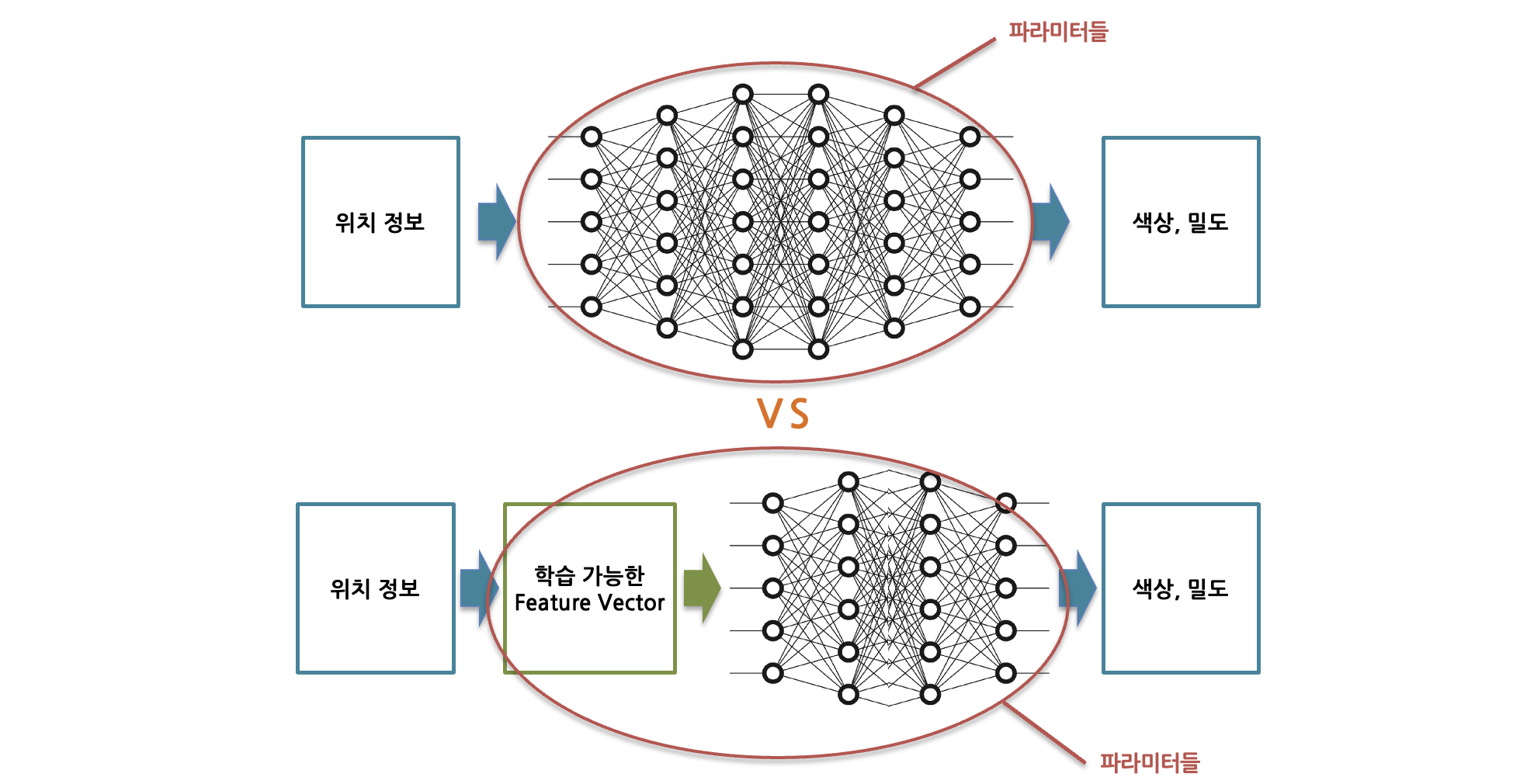
특정 자료구조에 ‘특징(feature)’ 정보를 인코딩하여 저장하고, 이러한 feature vector를 MLP의 파라미터와 마찬가지로 학습을 합니다. 딥러닝에서 한번의 iteration이 일어나는 과정에서 back-propagation 수행시 MLP상의 파라미터처럼 이 자료구조 내에 위치한 파라미터들도 업데이트 됩니다.
오직 MLP로만 3차원 정보를 표현하는 것에 비해서, parametric encoding을 도입할 경우 일반적으로 메모리 사용량은 증가하지만 연산량은 줄어들게 됩니다. 메모리 사용량이 증가하는 이유는 절대적인 파라미터 수가 증가하며 이를 적재할 메모리가 추가적으로 필요하기 때문입니다.
그렇다면 연산량이 줄어드는 이유는 무엇일까요? 첫 번째로는 필요로 하는 layer수가 감소하기 때문입니다. (그림6)의 왼쪽은 original NeRF를 설명한 그림이고, 오른쪽은 NeRF에 instant-NGP를 적용시킨 모습입니다. Original NeRF에서는 3차원 정보의 표현을 오로지 MLP에 의존합니다. 반면 instant-NGP를 적용할 경우, MLP에 진입하기 전에 조금 더 현실 좌표와 가까운 (덜 추상적인) 파라미터 묶음을 두기 때문에 투과하는 시간이 감소하게 됩니다. 또한, back-propagation을 통해 파라미터를 업데이트 할 때에도 chain rule을 통해 gradient를 계산해야 하는 양이 줄기 때문에 시간을 절약할 수 있습니다.
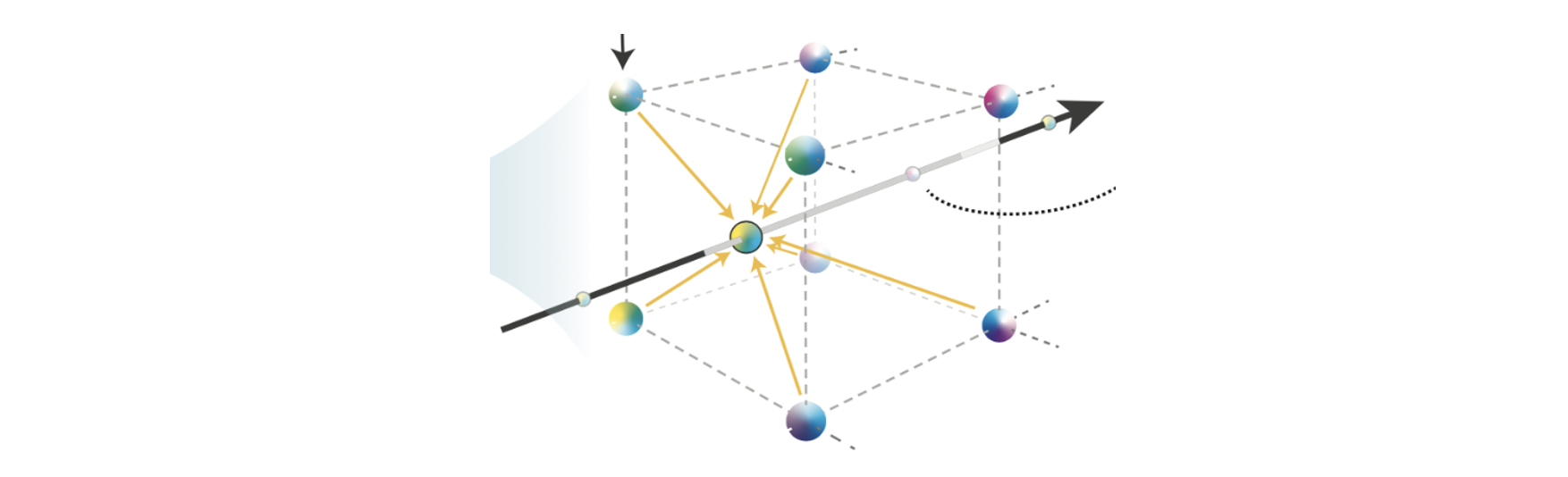
하지만 의문이 들지 않으신가요? 파라미터 수는 증가했다고 했습니다. 그렇다면 매 iteration마다 이 많아진 파라미터들을 업데이트 해야하기 때문에 연산량이 증가하는 것 아닐까요? 그렇지 않습니다. 그 이유를 설명드리겠습니다.
Back-propagation이 일어나는 과정을 생각해 봅시다. Fully connected layer와 다르게 parametric encoding에서는 다음 layer의 모든 파라미터의 변화에 대한 해당 파라미터의 변화율을 구하지 않습니다. 대신 주변 파라미터의 변화에 대한 변화율만을 구합니다. 따라서 파라미터 수가 많아진다고 하더라도 optimization중 일어나는 연산은 크게 늘어나지 않게 되는 것이죠. Parametric encoding에서는 딥러닝 네트워크와 다르게 각 파라미터(feature vector)들이 공간적인 상관관계를 내포하고 있기 때문에 이것이 가능합니다.
4. Dense & Sparse Parametric Encoding
NeRF에 parametric encoding을 어떻게 적용시킬 수 있을지에 대해 생각해 봅시다.
3차원 공간상의 서로 가까운 위치를 갖는 두 점은 parametric encoding이 쓰이는 자료구조에서 연관성 있는 위치에 존재해야 합니다. 우선, NeRF에서 학습하고자 하는 scene 에 대하여, 대응하는 3차원 feature grid의 각 칸에 feature정보를 담고 있는 파라미터를 할당한다고 생각해 봅시다.
Dense와 sparse parametric encoding의 가장 큰 차이점은 “물체가 존재하지 않는 non-interested 영역에 파라미터를 할당하는가?” 입니다. Dense parametric encoding에서는 모든 영역에 대해 feature vector를 담고 있기 때문에 메모리 사용량이 많아지게 됩니다. 입자가 없는 빈 공간에도 파라미터를 할당해야 해서 메모리를 낭비하게 됩니다.
특히, NeRF와 같은 3D reconstruction에 대해서 우리가 “보는” 시점에서 관심있는 것은 물체의 표면(surface)입니다. 표면은 평면이라고 볼수 있기 때문에 길이가 증가할수록 면적이 $ O(N^2) $ 만큼만 증가힙니다. 반면 dense parametric encoding을 사용할 경우 파라미터의 수는 불필요하게 $ O(N^3) $ 만큼 증가하기 때문에 낭비라고 볼 수 있죠.
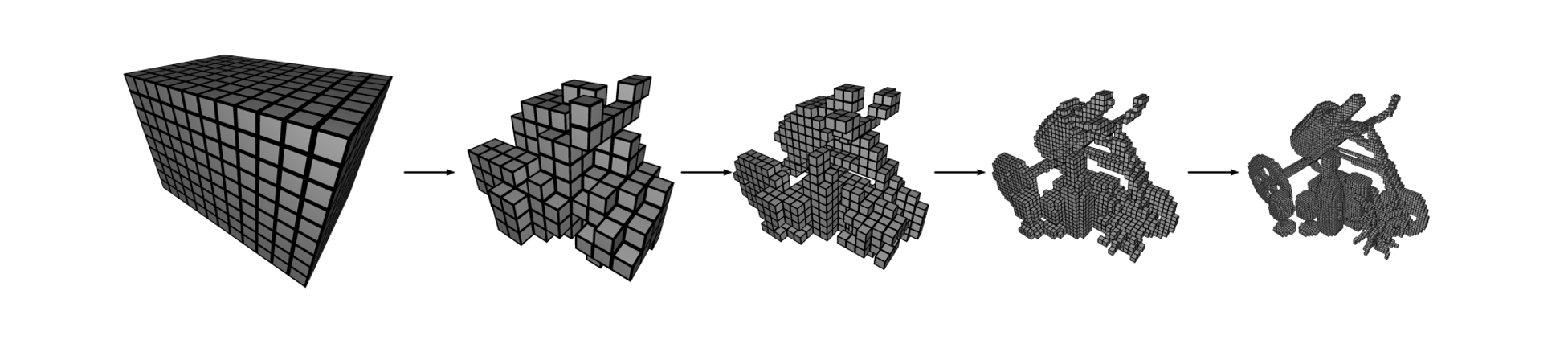
하지만 NeRF에서는 초기의 표면(surface)를 전혀 모릅니다. (NeRF에서는 이미지만을 갖고 학습하여, 깊이 정보를 사전에는 모르기 때문입니다.) 초기에 어떤 영역에 물체가 존재하는지 여부를 알아야 feature grid 상에서 일부 칸만 사용하는 sparse parametric encoding을 사용할 수 있는데 그렇지 못한 것이죠. NSVF와 같은 경우에는 학습이 일어나는 과정에서 점차적으로 feature grid가 잘려나가는 형식으로 이를 구현했습니다.
Instant-ngp에서는 sparse parametric encoding을 구현하기 위한 NSVF와는 다른 획기적인 방법을 고안해 냈는데요, 다음 단원에서 알아보시죠.
5. Parametric Encoding in Instant-NGP
Parametric encoding에서 feature vector는 앞서 살펴봤던 grid 이외에도 octree, voxel 등 다양한 자료 구조에 할당될 수 있습니다. 독특하게도, instant-NGP에서는 “해시 테이블(hash table)” 을 사용했습니다. 해시 테이블의 인덱스에 대응하는 값(value) 부분에 feature vector가 위치하는 구조입니다. 특정 좌표의 위치 정보를 종합하여 하나의 해시 테이블 인덱스로 매핑합니다. 구체적으로 어떤 알고리즘이 사용되었는지는 다음 단원을 참고해주세요.
해시 테이블을 사용함으로써 가지는 이점은 무엇이 있을까요? 첫 번째로, hash라는 자료 구조 특성상 query하는 속도가 매우 빠르다는 효과가 있습니다. 또한, 메모리 할당량을 컨텐츠와 상관없이, 그리고 뒤에 NeRF가 오던 gigapixel image가 오던 SDF가 오던 상관없이 정확한 값으로 설정할 수 있다는 장점이 있습니다. 이렇게 예측 가능한 메모리 구조를 사용함으로써 더욱 빠른 퍼포먼스를 낼 수 있다는 장점이 있습니다.
해시 테이블은 충돌(collision)이 발생할 수 있습니다. Instant-NGP에서는 multi-resolution이라는 이름으로 여러 단계를 두어 한 resolution에서 충돌이 발생하더라도 다른 resolution에서는 발생 안한다면 괜찮다는 시스템을 사용하여 안정성을 확보했습니다. 충돌 처리 알고리즘이 직접적으로 작동하지 않아도 파라미터들이 이를 반영하여 자동적으로 학습되는 방식을 사용했습니다.
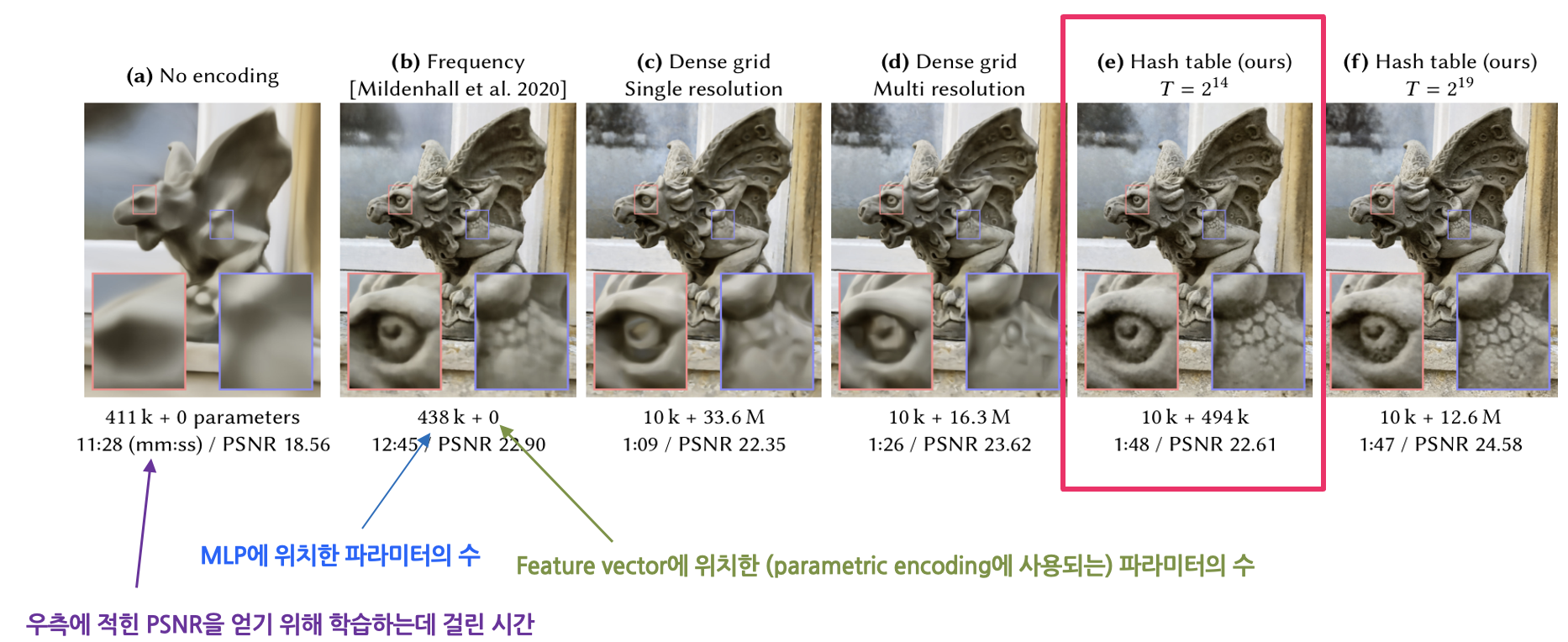
(그림9)는 parametric encoding을 적용했을 때, 특히 hash table에 feature vector를 할당했을 때 어떠한 효과가 있는지 여실히 보여줍니다. (a)는 아무런 인코딩을 하지 않았을 때의 모습이며, 고주파의 정보를 표현하지 못하는 것을 확인할 수 있습니다. (b)는 기존 NeRF에 사용된 frequency encoding을 적용한 모습입니다. MLP에 438k개의 파라미터가 존재하며, parametric encoding을 사용하지 않았기에 feature vector에 파라미터가 존재하지 않습니다. (c), (d)는 dense grid parametric encoding을 사용한 예시입니다. Grid의 모든 칸에 feature vector를 할당했기에, 파라미터 수가 매우 큰 것을 확인할 수 있습니다. (e)는 instant-NGP에서 채택한 hash table을 사용한 방식입니다. Dense grid를 사용한 것에 비해 파라미터 수가 획기적으로 감소했습니다. 또한 비슷한 퀄리티(PSNR)의 결과물을 얻기 위해 학습한 시간이 NeRF방식의 8분의 1 수준에 불과합니다. (f)는 (e)와 비슷하지만 해시 테이블의 크기를 늘린 결과인데, 시간 대비 품질은 증가하지만 사용되는 파라미터 수가 매우 증가하여 그닥 좋은 효과를 얻었다고 보기는 어렵습니다.
6. Multiresolution Hash Encoding

Instant-NGP의 neural nework를 $ m(y; \phi) $ 라고 할 때, parametric encoding 파트에서는 neural network 에 들어갈 y를 $ y = enc(x; \theta) $ 와 같이 찾는 과정입니다.($ \phi $ 는 MLP에 위치한 파라미터이며, $ \theta $ 는 인코딩에 쓰이는 파라미터입니다.) 해시 테이블을 사용한 parametric encoding 과정은 다음과 같습니다.
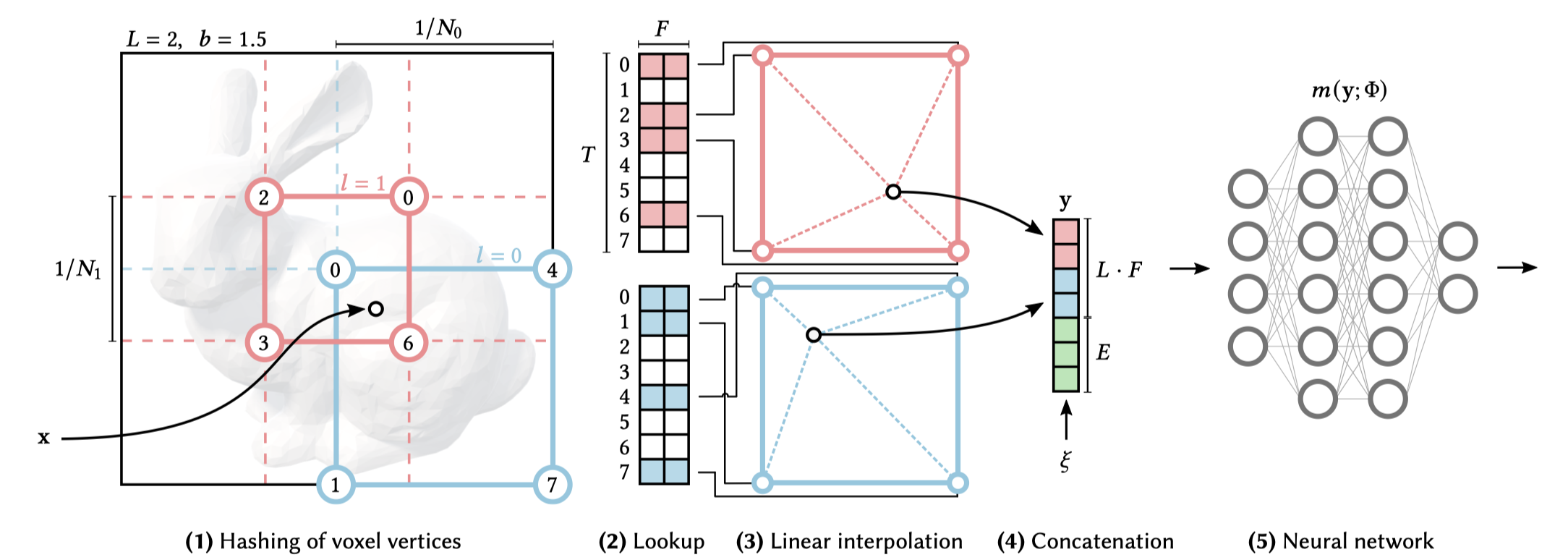
1. L개의 d차원 grid가 정의됨
학습하고자 하는 scene 상의 좌표를 grid로 생각합니다. $ L $을 level의 수 라고 하면, 우리는 이 grid를 $ L $개 정의할 것입니다. 각 grid는 고유의 resolution을 갖습니다. (현재 상황: L개의 grid가 있고, 각 grid는 고유의 resolution을 갖음.) 사실 NeRF의 scene은 3D ($ d = 3 $)이지만 편의상 (그림11)에서는 2D ($ d = 2 $)라고 가정했습니다.
(그림11)을 보면 2차원 grid를 2개 정의했습니다(빨간색, 파란색). 따라서 $ L = 2 $ 입니다. 파란색 grid는 더 낮은 level($ l = 0 $)이며 2x2 resolution을 갖습니다. 2등분 되어 있으므로 $ N_0 = 2 $ 라고 할 수 있죠. 빨간색 grid는 더 높은 level($ l = 1 $)이며 3x3 resolution을 갖습니다. 3등분 되어 있으므로 $ N_1 = 3 $ 입니다.
2. 각 level에 Hash Table에 할당되어 있음
각 level에는 hash table이 하나씩 할당됩니다. 해시 테이블의 크기는 $ T $입니다. ($ T $는 hyperparameter). 그리고 해시 테이블의 각 인덱스에는 feature vector가 할당됩니다. 이 feature vector는 인코딩 과정의 파라미터로써 back-propagation시 학습이 일어나게 됩니다.
(그림11)에서는 해시 테이블의 원소가 7개 이므로 $ T = 7 $이며, 테이블의 각 칸에 위치하는 feature vector의 크기가 2이므로 $ F = 2 $입니다.
3. Scene의 좌표가 해시 함수를 거쳐 테이블의 인덱스로 매핑됨
Input으로 주어지는 점 x가 있습니다. 각 level별로 그 점 x를 둘러싸는 격자상의 4개의 좌표로 치환됩니다. (그림 11)에서 점 x는 파란색 level($ l = 0 $)에서는 점 x를 둘러싸는 0, 4, 1, 7번 좌표로 치환됩니다 0, 4, 1, 7은 해시 함수에 통과된 이후 얻을 수 있는 해시 테이블의 인덱스 입니다. 빨간색 level($ l = 1 $)에서는 점 x를 둘러싸는 0, 2, 3, 6번 좌표로 치환됩니다. 마찬가지로 0, 2, 3, 6는
이때 사용되는 해시 함수는 아래와 같습니다.
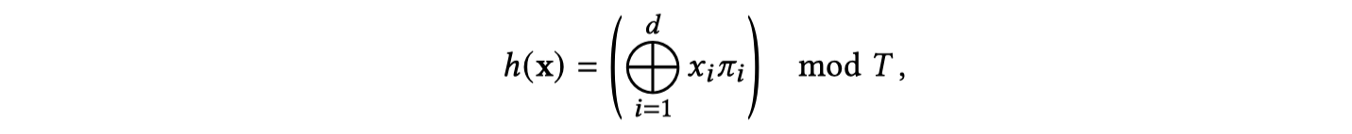
⊕는 bit-wise XOR연산이며, $ \pi $는 매우 큰 고유의 소수입니다. 이 해시 함수 연산 결과 매우 독립적인 임의의 수를 생성하게 됩니다.
이 과정을 거쳐서 결국 (그림11)의 입력 좌표 x에 대해, 각 level별로 4개의 해시 테이블 인덱스에 대응시킬 수 있습니다.
4. Feature Vector를 Interpolate
점 x의 각 level별로 4개의 해시 테이블 인덱스를 얻었는데, 이 인덱스에 해당하는 feature vector를 평균 내어 linear interpolate시킵니다. 이 과정을 통해 각 level별로 $ F $ 크기의 feature vector 하나를 얻을 수 있습니다.
5. 모든 Level의 feature vector를 연결하여 MLP의 입력값으로 주기
(그림11)의 (4)번 항목과 같이 여러 level의 interpolated된 feature vector를 연결합니다. 이와 더불어 $ 𝜉 $ 로 표현되는 viewing direction 등의 정보도 함께 연결되어 neural network의 input으로 주어집니다.
해시 함수를 사용하는데 어떻게 미분 가능할까?
Parametric encoding이란 주어지는 scene의 좌표가 인코딩된 feature vector도 마찬가지로 ‘학습’이 되는 과정이라고 했습니다. Instant-NGP에서는 feature vector도 마찬가지로 gradient를 구하여 업데이트를 하는데, loss로부터 back-propagation을 수행하여 chain rule을 통해 feature vector의 gradinet를 얻습니다. 랜덤값을 마구마구 뽑아내는 해시 함수를 사용하는데도 이러한 미분이 가능한 이유는, feature vector가 해시 함수를 거친 이후에 위치하는 덕분입니다. (그림11)을 다시 보시죠. (1)에서 해시 함수를 사용하지만 (2)번 과정에 feature vector가 위치합니다. Loss로부터 MLP를 거쳐 feature vector까지 back-propagation하는 동안에는 모두 미분 가능한 연산만 존재하므로 gradient-based 업데이트가 가능한 것입니다.
7. Hyperparameters

Resolution에 따라 grid를 여러 level 로 만든다고 했습니다. $ L $은 level의 수 입니다. $ L $값이 커질 수록 한 좌표에 대한 feature vector수가 증가하므로 품질은 올라가지만, 연산 시간 소모량이 커지며 메모리 사용량도 증가합니다.
$ N_{min} $과 $ N_{max} $는 이때 resolution의 최솟값과 최댓값을 나타냅니다. resolution이 작을수록 격자가 듬성듬성 있는 level이며, 클수록 격자가 조밀조밀한 level입니다.
$ N_{min} $과 $ N_{max} $가 주어졌으면 다음과 같이 $ l $번째 레벨의 resolution $ N_l $ 이 지정됩니다.
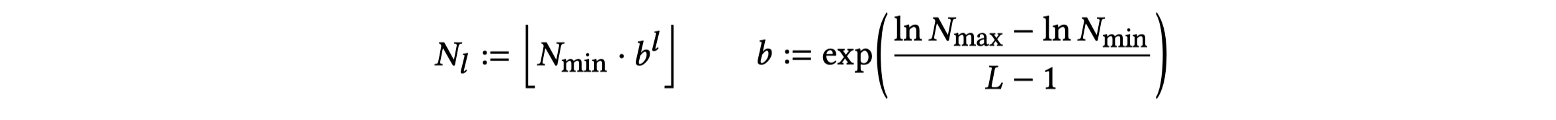
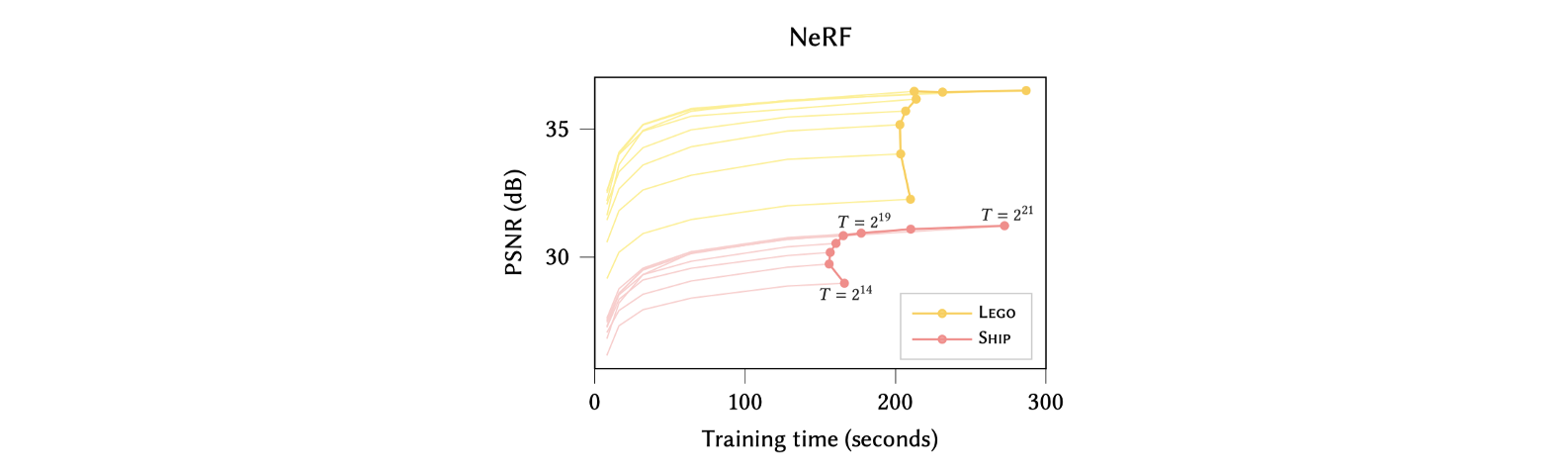
$ T $는 해시 테이블의 크기를 나타냅니다. 한 level당 해시 테이블 하나가 할당된다고 했는데, 이 해시 테이블의 인덱스 수를 $ T $라는 hyperparameter로 관리합니다. 위와 같이 경험적인(heuristic) 방법으로 실험을 통해 가장 적절한 $ T $값을 찾았습니다. (그림13)을 보시면, $ T $의 값을 증가시키면 NeRF에서 중간 뷰 합성시의 PSNR 값이 올라기지만, $ 2^{19} $를 기점으로 얻는 이득 대비 지나치게 학습시간이 늘어나는 문제를 보입니다.
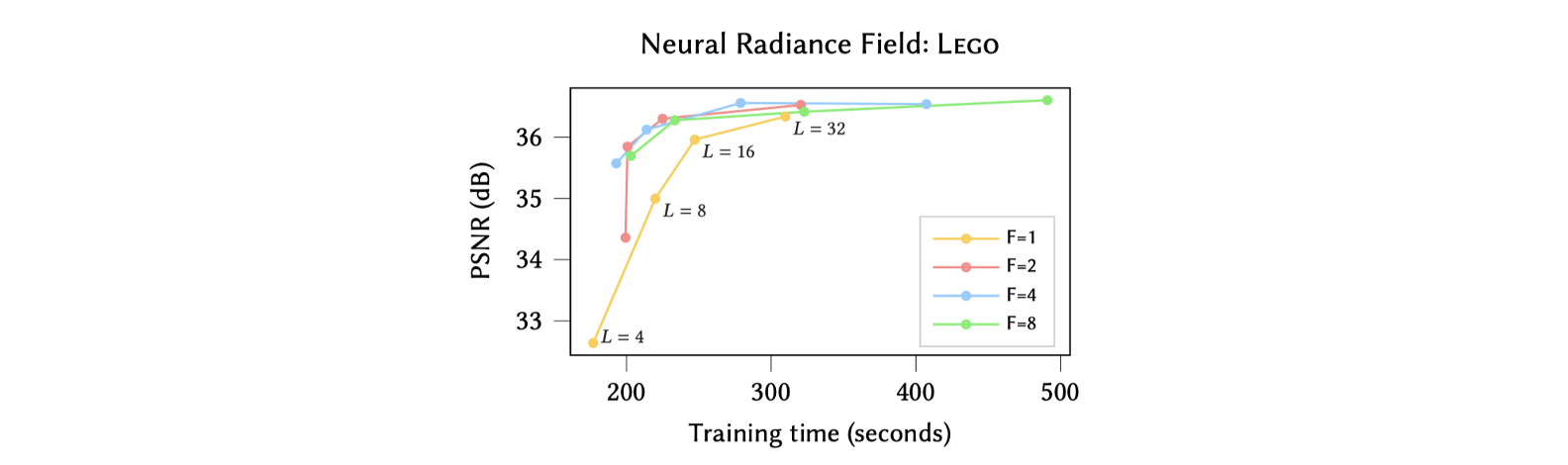
$ F $는 해시 테이블의 한 인덱스에 대응되는 feature vector의 크기입니다. $ F $와 $ L $ 또한 heuristic한 방법으로 적절한 값을 찾았습니다. Level수가 증가할 수록 측정된 PSNR값은 증가하지만 학습에 소요되는 시간도 같이 증가하는 것을 알 수 있습니다. $ L = 16 $이 선택되었습니다. 그리고, 그래프의 색상은 $ F $의 값을 나타내는데 이 중 빨간색 그래프 ($ F = 2 $일 때)가 가장 좋은 좌상단에 그래프가 위치하는 좋은 결과를 나타내기에 선택되었습니다.
8. 구현상의 특징
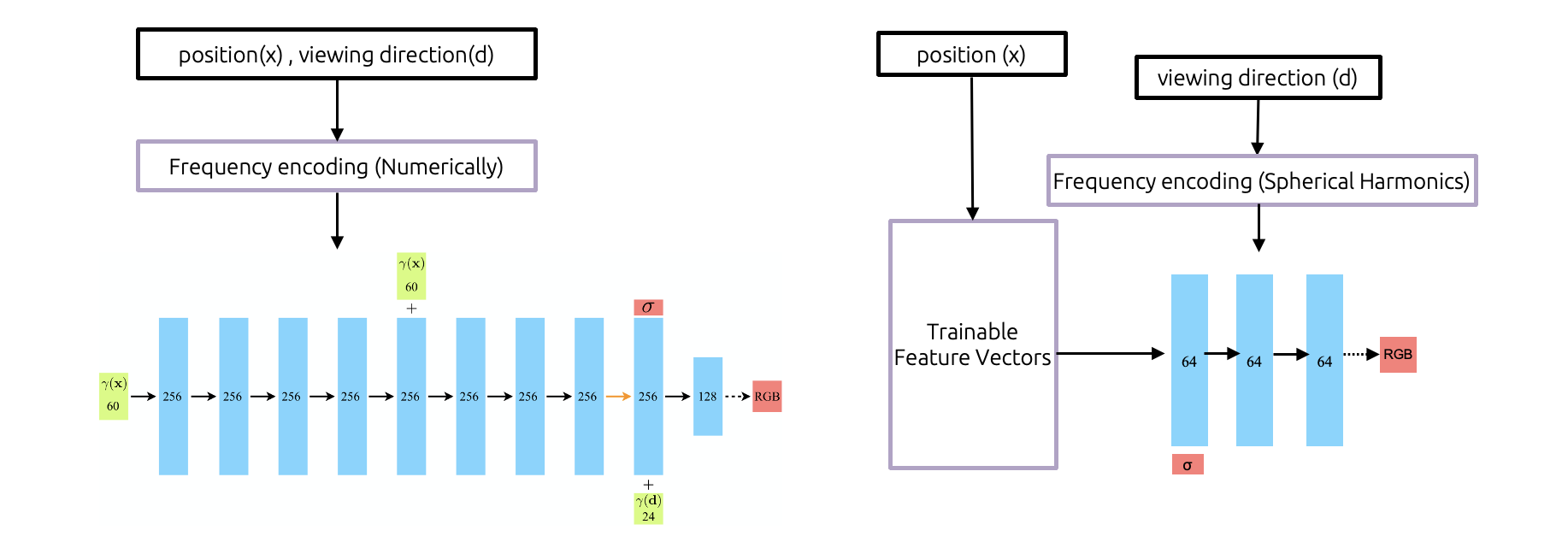
Instant-NGP는 Gigapixel images, NRC, SDF 등에도 적용할 수 있지만, NeRF에 적용하였을 때를 기준으로 구현상의 특징을 설명하겠습니다. Original NeRF를 그대로 가져왔다고 봐도 무방하지만 네트워크 구조가 훨씬 가벼워졌습니다.

NeRF와 마찬가지로 ‘위치 정보’를 통해 밀도(density)를 출력하는 전반부와 ‘바라보는 방향 정보’를 추가적으로 입력받아 색상(Color)을 출력하는 후반부로 나뉩니다. 위치에 대한 density정보가 출력된 이후, 바라보는 방향 정보가 spherical harmonics basis에 의해 인코딩되어 후반부의 MLP에 입력됩니다.
Density를 출력하는 전반부 layer 1개와 color를 출력하는 후반부 layer 2개가 연결되어, 총 3개의 hidden layer로 구성됩니다. 각 layer는 64개의 노드를 가집니다. (그림15)를 보았을 때, NeRF와 비교했을 때 layer의 개수가 대폭 줄어들었으며 layer 내 뉴런의 수도 감소하는 등 훨씬 간결해 진 것을 확인할 수 있습니다.
또한, 주어진 좌표에 대한 예측값을 얻어내기 위한 ray tracing이 일어나는 과정에서도 최적화 과정이 추가되었습니다. 빈 공간과 비어있지 않은 공간을 대략적으로 표시하는 “occupancy grid”를 두어, 샘플링시 물체가 존재하지 않는 구간에 대한 불필요한 연산이 일어나는 것을 최소화하도록 구현했습니다.
9. 결과 비교 및 결론
논문에서는 Instant-NGP를 적용한 NeRF를 original NeRF, mip-NeRF, NSVF와 비교합니다.
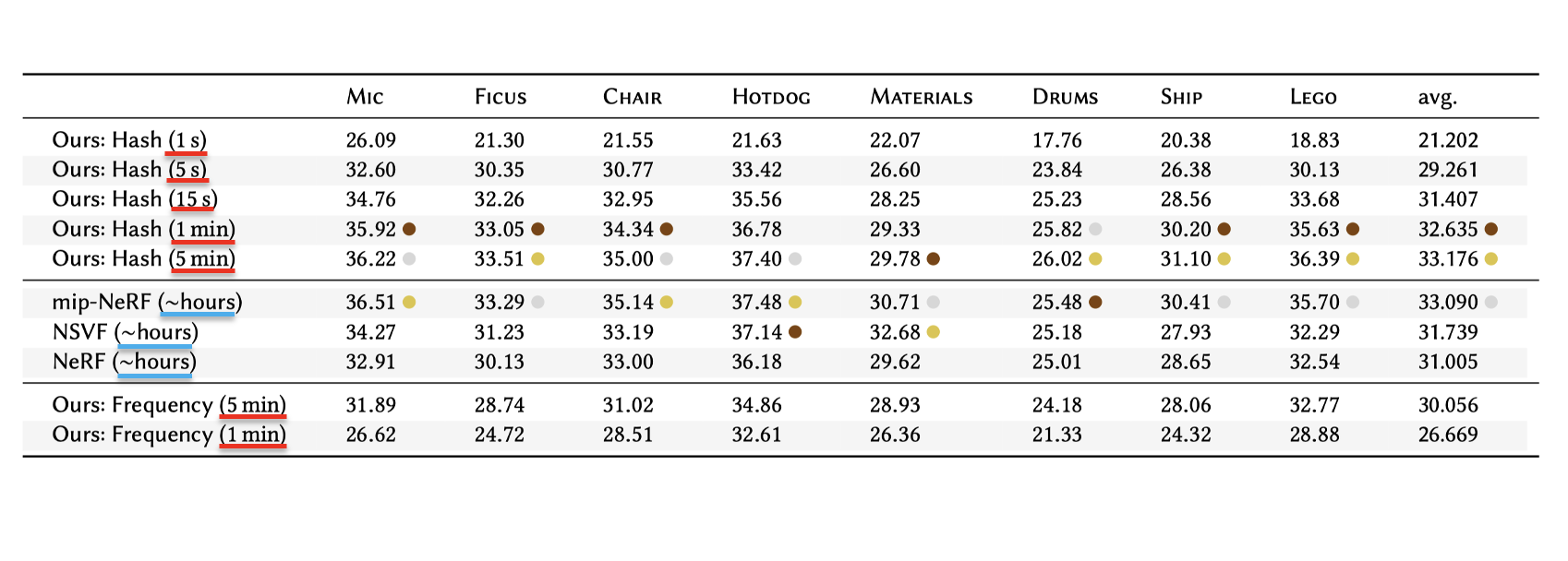
“Ours: Hash”가 Instant-NGP에 multiresolution hash enoding을 사용한 케이스 입니다. PSNR값만 비교해 보면 mip-NeRF나 NSVF이 더 좋은게 아닌가 착각할 수 있지만, 왼쪽 괄호 안에 쓰여진 학습 소요 시간을 확인해 보시면 생각이 달라집니다. mip-NeRF나 NSVF은 몇 시간 단위로 학습을 해서 해당 PSNR이 얻어진 것에 비해, instant-NGP에서는 고적 몇 초, 몇 분만에 얻어냈습니다. 이처럼 매우 빠른 시간 안에 높은 퀄리티의 렌더링 결과물을 뽑아낼 수 있는 모델을 만들 수 있다는 것이 instant-NGP의 가장 큰 장점이라고 할 수 있죠.
Instant-NGP는 고질적인 학습 시간의 문제점을 갖고 있던 implicit neural representation 방식에 hash table 기반의 parametric encoding을 접목시킴으로써 획기적인 속도의 개선을 이끌어냈습니다. 그렇기 때문에 실시간성을 요구하는 실사 기반의 그래픽을 구현하는 task에 유용하게 사용될 수 있을 것 같습니다.
논문에서는 개선점으로 ‘해시 함수’를 주목합니다. Collision을 예방할 수 있는 더 정교한 해시 함수를 선택하는 것을 넘어, 해시 함수 또한 학습을 통해 최적화하는 아이디어를 제시하고 있습니다(Dictionary-learning approach). 또한, 본 논문의 핵심 아이디어인 multiresolution has encoding을 다른 작업(attention-based task 등)에 쓰일 수 있도록 확장하는 것도 목표로 하고 있습니다.

댓글남기기